若复数 是纯虚数(
是纯虚数( 是虚数单位,
是虚数单位, 是实数),则
是实数),则 ( )
( )
A. B.
B. C.
C. D
D
设集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知 、
、 、
、 分别为
分别为 的三个内角
的三个内角 、
、 、
、 所对的边,若
所对的边,若 ,
, ,
, ,则 ( )
,则 ( )
A. |
B. |
C. |
D. |
在各项都为正数的等比数列 中,
中, ,前三项的和为
,前三项的和为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
“ ”是“直线
”是“直线 与直线
与直线 互相垂直”的( )
互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在 中,已知
中,已知 是
是 边上的一点,若
边上的一点,若 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
阅读如图程序框图,若输入的 ,则输出的结果是( )
,则输出的结果是( )
A. |
B. |
C. |
D. |
某校 名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分( )
名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分( )
A. |
B. |
C. |
D. |
已知 、
、 满足
满足 ,且
,且 的最大值是最小值的
的最大值是最小值的 倍,则
倍,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
若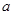 、
、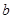 是方程
是方程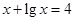 ,
,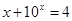 的解,函数
的解,函数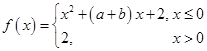 ,则关于
,则关于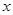 的方程
的方程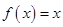 的解的个数是( )
的解的个数是( )
A.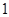 |
B. |
C.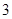 |
D.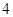 |
已知双曲线 的离心率是
的离心率是 ,则
,则 的值是 .
的值是 .
如图是一个空间几何体的三视图,则该几何体的体积为 .
给出下列四个命题:
①函数 有最小值是
有最小值是 ;
;
②函数 的图象关于点
的图象关于点 对称;
对称;
③若“ 且
且 ”为假命题,则
”为假命题,则 、
、 为假命题;
为假命题;
④已知定义在 上的可导函数
上的可导函数 满足:对
满足:对 ,都有
,都有 成立,
成立,
若当 时,
时, ,则当
,则当 时,
时, .
.
其中正确命题的序号是 .
在极坐标中,圆 的圆心
的圆心 到直线
到直线 的距离为 .
的距离为 .
如图,平行四边形 中,
中, ,
, 的面积为
的面积为 ,则平行四边形
,则平行四边形 的面积为
的面积为  .
.
设向量 ,
, ,
, .(1)若
.(1)若 ,求
,求 的值;
的值;
(2)设函数 ,求
,求 的最大、最小值.
的最大、最小值.
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为 .
.
| |
优秀 |
非优秀 |
合计 |
| 甲班 |
 |
|
|
| 乙班 |
|
 |
|
| 合计 |
|
|
 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否有 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的 名学生从
名学生从 到
到 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到 号或
号或 号的概率.
号的概率.
如图,已知矩形 中,
中, ,
, ,将矩形沿对角线
,将矩形沿对角线 把
把 折起,使
折起,使 移到
移到 点,且
点,且 在平面
在平面 上的射影
上的射影 恰好在
恰好在 上.
上.
(1)求证: ;
;
(2)求证:平面 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
在数列 中,
中, ,
, ,
, 对任意
对任意 成立,令
成立,令 ,且
,且 是等比数列.
是等比数列.
(1)求实数 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)求和: .
.
已知椭圆 的离心率为
的离心率为 ,直线
,直线 与以原点为圆心、椭圆
与以原点为圆心、椭圆 的短半轴长为半径的圆
的短半轴长为半径的圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)如图, 、
、 、
、 是椭圆
是椭圆 的顶点,
的顶点, 是椭圆
是椭圆 上除顶点外的任意点,直线
上除顶点外的任意点,直线 交
交 轴于点
轴于点 ,直线
,直线 交
交 于点
于点 ,设
,设 的斜率为
的斜率为 ,
, 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值.
设 ,函数
,函数 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 的单调区间;
的单调区间;
(3)当 时,求函数
时,求函数 在
在 上的最小值.
上的最小值.