已知集合 =( )
=( )
A. |
B. |
C. |
D.{—2,0} |
复数 (
( 是虚数单位)是实数,则x的值为( )
是虚数单位)是实数,则x的值为( )
| A.3 | B. |
C.0 | D. |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 是三个互不重合的平面,
是三个互不重合的平面, 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A.若 ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. |
B. |
C. |
D. |
设 为等差数列
为等差数列 的前
的前 项和,
项和, ,则
,则 = ( )
= ( )
A. |
B. |
C. |
D.2 |
设函数 ,则不等式
,则不等式 的解集是 ( )
的解集是 ( )
A. |
B. |
C. |
D. |
已知向量 ,向量
,向量 ,则
,则 的最大值和最小值分别为( )
的最大值和最小值分别为( )
A. |
B. |
C. |
D. |
已知抛物线 的焦点
的焦点 与双曲线
与双曲线 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为 ,且
,且 与
与 轴垂直,则此双曲线的离心率为( )
轴垂直,则此双曲线的离心率为( )
A. |
B.2 | C.  |
D. |
已知函数 有两个极值点
有两个极值点 ,若
,若 ,则关于
,则关于 的方程
的方程 的不同实根个数为( )
的不同实根个数为( )
| A.3 | B.4 | C.5 | D.6 |
已知函数 则
则 .
.
若程序框图如图所示,则该程序运行后输出的值是 .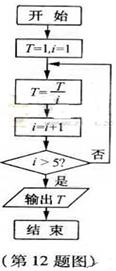
袋中共有6个除了颜色外完全相同的球,其中有1个红球, 2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于 .
若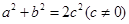 ,则直线
,则直线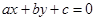 被圆
被圆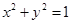 所截得的弦长为 .
所截得的弦长为 .
已知点 为
为 所在平面上的一点,且
所在平面上的一点,且 ,其中
,其中 为实数,若点
为实数,若点 落在
落在 的内部,则
的内部,则 的取值范围是 .
的取值范围是 .
若关于 的不等式
的不等式 在区间
在区间 上有解,则实数
上有解,则实数 的取值范围为 .
的取值范围为 .
若函数f(x)=x2+ax+2b在区间(0,1),(1,2)内各有一个零点,则 的取值范围是 .
的取值范围是 .
在△ABC中,内角A,B,C的对边分别为a,b,c,且满足 (a-c)cosB=bcosC.
(1)求角B的大小;(2)若b=,求△ABC面积的最大值.
数列 的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
(1)当实数 为何值时,数列
为何值时,数列 是等比数列?
是等比数列?
(2)在(1)的结论下,设 是数列
是数列 的前
的前 项和,求
项和,求 的值.
的值.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.
(Ⅰ)证明EF//平面A1CD;
(Ⅱ)证明平面A1CD⊥平面A1ABB1;
(Ⅲ)求直线BC与平面A1CD所成角的正弦值.
已知椭圆 :
: ,过点
,过点 作圆
作圆 的切线
的切线 交椭圆
交椭圆 于A,B两点。
于A,B两点。
(1)求椭圆 的焦点坐标和离心率;
的焦点坐标和离心率;
(2)求 的取值范围;
的取值范围;
(3)将 表示为
表示为 的函数,并求
的函数,并求 的最大值.
的最大值.
已知函数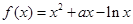 ,
,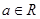 ;
;
(1)当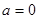 时,求函数
时,求函数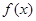 的单调区间;
的单调区间;
(2)若函数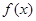 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数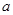 的取值范围;
的取值范围;
(3)令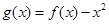 ,是否存在实数
,是否存在实数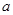 ,当
,当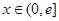 (
(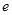 是自然对数的底数)时,函数
是自然对数的底数)时,函数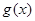 的最小值是
的最小值是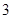 .若存在,求出
.若存在,求出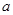 的值;若不存在,说明理由.
的值;若不存在,说明理由.