已知集合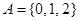 ,
,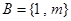 .若
.若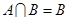 ,则实数
,则实数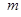 的值是( )
的值是( )
A. |
B. |
C. 或 或 |
D. 或 或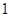 或 或 |
命题 :对任意
:对任意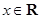 ,
,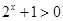 的否定是( )
的否定是( )
A.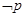 :对任意 :对任意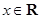 , ,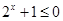 |
B.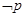 :不存在 :不存在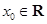 , ,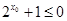 |
C.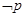 :存在 :存在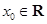 , ,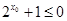 |
D.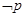 :存在 :存在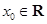 , ,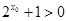 |
执行如图所示的程序框图,则输出的 值为( )
值为( )
| A.91 | B.55 | C.54 | D.30 |
若 ,则( )
,则( )
A. |
B. |
C. |
D. |
由直线 ,
, ,
, 与曲线
与曲线 所围成的图形的面积等于( )
所围成的图形的面积等于( )
A. |
B. |
C. |
D. |
已知平面向量 ,
, ,
, ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.向量 与向量 与向量 共线 共线 |
B.若 ( ( , ,  ),则 ),则 , , |
C.对同一平面内任意向量 ,都存在实数 ,都存在实数 , , ,使得 ,使得 |
D.向量 在向量 在向量 方向上的投影为 方向上的投影为 |
若函数 的图象与函数
的图象与函数 的图象至多有一个公共点,则实数
的图象至多有一个公共点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
同时满足以下4个条件的集合记作 :(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
:(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
 的等差数列.那么
的等差数列.那么 中元素的个数是( )
中元素的个数是( )
| A.96 | B.94 | C.92 | D.90 |
在公比小于零的等比数列 中,
中, ,
, ,则数列
,则数列 的前三项和
的前三项和 .
.
函数
 的最小值是 .
的最小值是 .
曲线 在点
在点 处的切线经过点
处的切线经过点 ,则
,则 ______.
______.
已知平面向量 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 ;若平行四边形
;若平行四边形 满足
满足 ,
,

 ,则平行四边形
,则平行四边形 的面积为 .
的面积为 .
已知函数 若
若 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
已知函数 (
( ),数列
),数列 满足
满足 ,
, ,
, .则
.则 与
与 中,较大的是 ;
中,较大的是 ; ,
, ,
, 的大小关系是 .
的大小关系是 .
已知函数 .
.
(Ⅰ)求函数 的最小正周期及最小值;
的最小正周期及最小值;
(Ⅱ)若 ,且
,且 ,求
,求 的值.
的值.
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且
,且 .
.
(Ⅰ)若 ,求
,求 的面积;
的面积;
(Ⅱ)若 ,求
,求 的最大值.
的最大值.
已知等差数列 的前
的前 项和为
项和为 ,
, ,且
,且 ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,求
,求 的值和
的值和 的表达式.
的表达式.
已知函数 ,
, .
.
(Ⅰ)若函数 的图象与
的图象与 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;
(Ⅱ)若函数 在
在 上存在零点,求
上存在零点,求 的取值范围;
的取值范围;
(Ⅲ)设函数 ,
, .当
.当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
已知函数 ,
, .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)设 ,
, ,
, ,
, 为函数
为函数 的图象上任意不同两点,若过
的图象上任意不同两点,若过 ,
, 两点的直线
两点的直线 的斜率恒大于
的斜率恒大于 ,求
,求 的取值范围.
的取值范围.
如果项数均为 的两个数列
的两个数列 满足
满足 且集合
且集合 ,则称数列
,则称数列 是一对“
是一对“ 项相关数列”.
项相关数列”.
(Ⅰ)设 是一对“4项相关数列”,求
是一对“4项相关数列”,求 和
和 的值,并写出一对“
的值,并写出一对“ 项相
项相
关数列” ;
;
(Ⅱ)是否存在“ 项相关数列”
项相关数列” ?若存在,试写出一对
?若存在,试写出一对 ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅲ)对于确定的 ,若存在“
,若存在“ 项相关数列”,试证明符合条件的“
项相关数列”,试证明符合条件的“ 项相关数列”有偶数对.
项相关数列”有偶数对.