全集
则
（ ）
A． |
B． |
C． |
D． |
已知命题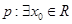
，
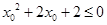，则
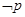为 （ ）
A． |
B． |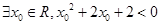
C． |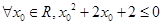
D． |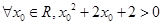
在ΔABC中，角A、B、C所对的对边长分别为a、b、c，sinA、sinB、sinC成等比数列，且c= 2a，则cosB的值为（ ）
A.
B.
C.
D.
设函数
是R上的单调递减函数，则实数a的取值范围为( )
| A．(-∞，2) | B．(-∞， ] |
C．(0,2) | D．[,2) |
函数
的最小正周期是
，若其图像向右平移
个单位后得到的函数为奇函数，则函数
的图像（ ）
A．关于点 对称 |
B．关于直线 对称 |
C．关于点 对称 |
D．关于直线 对称 |
已知函数
是
上的偶函数，若对于
，都有
，且当
时，
，则
（ ）
A． |
B． |
C． |
D．1 |
某四面体的三视图如图所示．该四面体的六条棱的长度中，最大的是（ ）
A． |
B． |
C． |
D． |
在R上定义运算
若对任意
，不等式
都成立，则实数
的取值范围是（ ）
A． |
B． |
C． |
D． |
已知函数
, 则
的值是 .
若函数
在
处有极值，则函数
的图象在
处的切线的斜率为 .
由曲线f(x)＝
与
轴及直线
围成的图形面积为
，则
的值为 .
若关于x的不等式
的解集为空集，则实数a的取值范围是 .
定义在R上的函数
满足：
，且对于任意的
,都有
＜
，则不等式
＞
的解集为 .
已知曲线
交于点P，若设曲线y=f（x）在点P处的切线与x轴交点的横坐标为
的值为 .
函数
的定义域为D，若存在闭区间[a，b]
D，使得函数满足：(1)在[a，b]内是单调函数；(2)在[a，b]上的值域为[2a，2b]，则称区间[a，b]为y=的“美丽区间”．下列函数中存在“美丽区间”的是 . (只需填符合题意的函数序号)
①、
； ②、
；
③、
； ④、
.
在
中，
分别是角
的对边，
，
；
（Ⅰ）求
的值；
（Ⅱ）若
，求边
的长.
若
是定义在
上的增函数，且
（1）、求
的值；（2）、若
，解不等式
.
已知函数
＞0，
＞0，
＜
的图像与
轴的交点为（0，1），它在轴右侧的第一个最高点和第一个最低点的坐标分别为
和
（1）求
的解析式及
的值；
（2）若锐角
满足
，求
的值.
某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为
立方米，且
．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为
千元，设该容器的建造费用为
千元．
（Ⅰ）写出关于
的函数表达式，并求该函数的定义域；
（Ⅱ）求该容器的建造费用最小时的．
已知函数
，
．
（Ⅰ）设
（其中
是
的导函数），求
的最大值；
（Ⅱ）求证:当
时，有
；
（Ⅲ）设
,当
时,不等式
恒成立，求
的最大值.