若集合
，
，则集合
等（ ）
A． |
B． |
C． |
D． |
已知
为虚数单位，复数
，则复数
在复平面内的对应点位于 （ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
函数
的定义域是 （ ）
A． |
B． |
C． |
D． |
如果等差数列
中，
则
（ ）
| A．14 | B．21 | C．28 | D．35 |
已知命题p：
（ ）
A． |
B． |
C． |
D． |
函数
的图象是 （ ）
下列函数中，既是奇函数，又在(0，
）上单调递减的函数是 ( )
A． |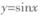
B． |
C． |
D． |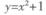
函数
的零点所在的一个区间是 （ ）
A． |
B． |
C． |
D． |
若
则
（ ）
A． |
B． |
C． |
D． |
已知函数
且
是递增数列，那么实数a的取值范围是 （ ）
A． |
B． |
C． |
D． . |
已知
都是正实数， 函数
的图象过（0,2）点，则
的最小值是（ ）
A． |
B． |
C． |
D． |
若关于x的方程
有两个不相等的实数解，则实数m的取值范围是（ ）
A． |
B． |
C． |
D． |
若
其中
为虚数单位，则
____________．
已知
函数
上为增函数，则实数
的取值范围是 .
已知函数
是
上的偶函数，对任意
，都有
成立， 当
且
时，都有
给出下列命题：
①
且
是函数
的一个周期；②直线
是函数的一条对称轴；
③函数在
上是增函数； ④函数在
上有四个零点. 其中正确命题的序号为___________（把所有正确命题的序号都填上）
(本小题满分10分)
已知
．
（1）求
的值；
（2）求
的值．
(本小题满分12分)
已知函数
．
（1）求
的单调递增区间；
（2）求的最大值及取得最大值时相应的
的值．
已知
是一个等差数列，且
，
。
（1）求的通项
；
（2）求的前
项和
的最大值．
（本小题满分12分）已知等差数列
为递增数列，且
是方程
的两根，数列
的前
项和
；
（1）求数列和的通项公式；
（2）若
，
为数列
的前n项和，证明：
(本小题满分12分)
已知函数
的图象过坐标原点O,且在点
处的切线的斜率是
（1）求实数
的值；
（2）求
在区间
上的最大值；
（3）对任意给定的正实数
，曲线
上是否存在两点P、Q，使得
是以O为直角顶点的直角三角形，且此三角形斜边中点在
轴上？说明理由．
已知函数
．
（Ⅰ）试求
的值域；
(Ⅱ)设
若对
， 
，恒
成立，试求实数
的取值范围