不等式
的解集是( )
A． |
B． |
C． |
D． |
命题“存在
使得
”的否定是（ ）
A．不存在使得 |
B．对任意， |
| C．对任意， |
D．存在，使得 |
已知三条不重合的直线
，两个不重合的平面
，有下列命题：
①若
，且
，则
②若
，且，则
③若
，
，则
④若
，则
其中真命题的个数是（ ）
| A．4 | B．3 | C．2 | D．1 |
若不等式
对任意实数
均成立，则实数
的取值范围是（ ）
A． |
B． |
C． |
D． |
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则该几何体的体积为（ ）
| A．9 | B．10 | C．11 | D． |
设向量
，记
，函数
的周期是（ ）
A． |
B． |
C． |
D． |
设偶函数
满足：当
时，
，则
=（ ）
A． |
B． |
C． |
D． |
在等比数列
中，
是
的等差中项，公比
满足如下条件：
（
为原点）中，
，
，
为锐角，则公比等于（ ）
| A．1 | B．-1 | C．-2 | D． |
一个正四棱锥和一个正四面体的所有棱长都相等，将它们的一个三角形重合在一起，组成一个新的几何体，则新几何体是（ ）
| A．五面体 | B．六面体 | C．七面体 | D．八面体 |
一个棱长为6的正四面体纸盒内放一个正方体，若正方体可以在纸盒内任意转动，则正方体棱长的最大值为（ ）
| A．2 | B．3 | C． |
D． |
已知向量
，则向量
与
的夹角
的余弦值为 .
设实数
满足不等式组
，则目标函数
的最小值为 .
若正数
满足
，则
的最小值为 .
在平面几何中，有这样一个定理：过三角形的内心作一直线，将三角形分成的两部分的周长比等于其面积比.请你类比写出在立体几何中，有关四面体的相似性质： .
已知正方体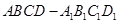
的棱长为1，动点P在正方体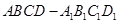表面上运动，且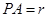
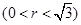，记点P的轨迹长度为
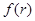，则
.
设不等式
的解集为M.
（1）如果
，求实数
的取值范围；
（2）如果
，求实数的取值范围.
如图，在直三棱柱
中，
,点
分别为
和
的中点.
（1）证明：
平面
；
（2）求
和
所成的角.
已知数列
为等差数列，数列
为等比数列且公比大于1，若
，
，且
恰好是一各项均为正整数的等比数列的前三项.
（1）求数列，的通项公式；
（2）设数列
满足
，求
.
已知函数
（
均为正常数），设函数
在
处有极值.
（1）若对任意的
，不等式
总成立，求实数
的取值范围；
（2）若函数在区间
上单调递增，求实数
的取值范围.
（如图1）在平面四边形
中，
为
中点，
，
，且
，现沿
折起使
，得到立体图形（如图2），又B为平面ADC内一点，并且ABCD为正方形，设F，G，H分别为PB，EB，PC的中点.
（1）求三棱锥
的体积；
（2）在线段PC上是否存在一点M，使直线
与直线
所成角为
？若存在，求出线段的长；若不存在，请说明理由.
已知
是关于
的方程
的两个根，且
.
（1）求出
与
之间满足的关系式；
（2）记
，若存在
，使不等式
在其定义域范围内恒成立，求的取值范围.