直线 的倾斜角是 .
的倾斜角是 .
过点(0,1),且与直线2x+y-3=0平行的直线方程是_ .
已知直线 ,
, 互相垂直,则实数
互相垂直,则实数 的值是 .
的值是 .
已知空间点 ,且
,且 ,则点A到的平面yoz的距是 .
,则点A到的平面yoz的距是 .
圆 :
: +
+ =1,圆
=1,圆 与圆
与圆 关于直线
关于直线 对称,则圆
对称,则圆 的标准方程为 .
的标准方程为 .
已知a、b是不同的直线, 、
、 、
、 是不同的平面,给出下列命题:
是不同的平面,给出下列命题:
①若 ∥
∥ ,a
,a
 ,则a∥
,则a∥ ; ②若a、b与
; ②若a、b与 所成角相等,则a∥b;
所成角相等,则a∥b;
③若 ⊥
⊥ 、
、 ⊥
⊥ ,则
,则 ∥
∥ ; ④若a⊥
; ④若a⊥ , a⊥
, a⊥ ,则
,则 ∥
∥
其中正确的命题的序号是 .
直线 与圆
与圆 恒有交点,则实数a的取值范围是 .
恒有交点,则实数a的取值范围是 .
如图,在三棱锥 中,
中, 底面
底面 ,
, ,
, ,则
,则 与底面
与底面 所成角的正切值为 .
所成角的正切值为 .
已知 满足
满足 ,则
,则 的取值范围是 .
的取值范围是 .
空间四个点P、A、B、C在同一球面上,PA、PB、PC两两垂直,且PA=PB=PC=a,那么这个球的表面积是 .
设圆 上有且仅有两个点到直线
上有且仅有两个点到直线 的距离等于1,则圆半径r的取值范围 .
的距离等于1,则圆半径r的取值范围 .
圆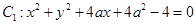 和圆
和圆 相内切,若
相内切,若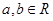 ,且
,且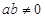 ,则
,则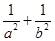 的最小值为 .
的最小值为 .
如图,一个圆锥形容器的高为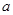 ,内装有一定量的水,如果将容器倒置,这时所形成的圆锥的高恰为
,内装有一定量的水,如果将容器倒置,这时所形成的圆锥的高恰为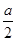 (如图2-②),则图2-①中的水面高度为 .
(如图2-②),则图2-①中的水面高度为 .
直线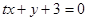 与圆
与圆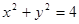 相交于A、B两点,若
相交于A、B两点,若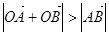 ,则实数t的范围 .
,则实数t的范围 .
已知直线经过点 ,求分别满足下列条件的直线方程:
,求分别满足下列条件的直线方程:
(1)倾斜角的正弦为 ;
;
(2)与两坐标轴的正半轴围成的三角形面积为4.
已知圆 及直线
及直线 . 当直线
. 当直线 被圆
被圆 截得的弦长为
截得的弦长为 时, 求(1)
时, 求(1) 的值; (2)求过点
的值; (2)求过点 并与圆
并与圆 相切的切线方程.
相切的切线方程.
如图,在四面体 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
(1)EF∥平面ACD;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)若平面 ⊥平面
⊥平面 ,且
,且 ,求三棱锥
,求三棱锥 的体积.
的体积.
(文)已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的标准方程;
(2)设直线
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,
,
(理)已知⊙ :
: 和定点
和定点 ,由⊙
,由⊙ 外一点
外一点 向⊙
向⊙ 引切线
引切线 ,切点为
,切点为 ,且满足
,且满足 .
.
(1)求实数 间满足的等量关系;
间满足的等量关系;
(2)求线段 长的最小值;
长的最小值;
(3)若以 为圆心所作的⊙
为圆心所作的⊙ 与⊙
与⊙ 有公共点,试求半径取最小值时的⊙
有公共点,试求半径取最小值时的⊙ 方程.
方程.
如图,直三棱柱 中,
中, 、
、 分别是棱
分别是棱 、
、 的中点,点
的中点,点 在棱
在棱 上,已知
上,已知 ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)设点 在棱
在棱 上,当
上,当 为何值时,平面
为何值时,平面 平面
平面 ?
?
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L⊥直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
试建立适当的直角坐标系,解决下列问题:
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。