已知全集 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知命题 、
、 ,则“
,则“
 为真”是“
为真”是“
 为真”的( )
为真”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
向量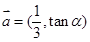 ,
,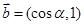 ,且
,且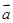 ∥
∥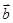 ,则
,则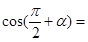 ( )
( )
A.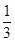 |
B.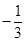 |
C.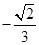 |
D.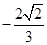 |
在正项等比数列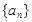 中,
中,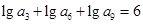 ,则
,则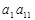 的值是( )
的值是( )
A.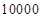 |
B.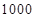 |
C.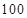 |
D.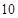 |
已知 且
且 ,函数
,函数 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
定义运算 ,若函数
,若函数 在
在 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知 满足
满足 ,则目标函数
,则目标函数 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D. |
已知 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
函数 的最大值是( )
的最大值是( )
A. |
B. |
C. |
D. |
已知等差数列 的公差
的公差 ,若
,若 (
( ),则
),则 ( )
( )
A. |
B. |
C. |
D. |
设 、
、 都是非零向量,下列四个条件中,一定能使
都是非零向量,下列四个条件中,一定能使 成立的是( )
成立的是( )
A. |
B. |
C. |
D. |
已知函数 的导函数图象如图所示,若
的导函数图象如图所示,若 为锐角三角形,则一定成立的是( )
为锐角三角形,则一定成立的是( )
A. |
B. |
C. |
D. |
已知函数 ,则
,则 .
.
若直线 与幂函数
与幂函数 的图象相切于点
的图象相切于点 ,则直线
,则直线 的方程为 .
的方程为 .
已知函数 是
是 上的奇函数,且
上的奇函数,且 的图象关于直线
的图象关于直线 对称,当
对称,当 时,
时, ,则
,则 .
.
若对任意 ,
, ,(
,( 、
、 )有唯一确定的
)有唯一确定的 与之对应,称
与之对应,称 为关于
为关于 、
、 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数 为关于实数
为关于实数 、
、 的广义“距离”:
的广义“距离”:
(1)非负性: ,当且仅当
,当且仅当 时取等号;
时取等号;
(2)对称性: ;
;
(3)三角形不等式: 对任意的实数z均成立.
对任意的实数z均成立.
今给出四个二元函数:
① ;②
;② ③
③ ;④
;④ .
.
能够成为关于的 、
、 的广义“距离”的函数的所有序号是 .
的广义“距离”的函数的所有序号是 .
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数 的图象.求
的图象.求 在区间
在区间 上零点的个数.
上零点的个数.
已知等比数列 为递增数列,且
为递增数列,且 ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)令 ,不等式
,不等式 的解集为
的解集为 ,求所有
,求所有 的和.
的和.
在 中,角
中,角 对边分别是
对边分别是 ,且满足
,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,
, 的面积为
的面积为 ;求
;求 .
.
已知函数 .
.
(Ⅰ)若函数 的值域为
的值域为 .求关于
.求关于 的不等式
的不等式 的解集;
的解集;
(Ⅱ)当 时,
时, 为常数,且
为常数,且 ,
, ,求
,求 的最小值.
的最小值.
某连锁分店销售某种商品,每件商品的成本为 元,并且每件商品需向总店交
元,并且每件商品需向总店交 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为 元时,一年的销售量为
元时,一年的销售量为 万件.
万件.
(Ⅰ)求该连锁分店一年的利润 (万元)与每件商品的售价
(万元)与每件商品的售价 的函数关系式
的函数关系式 ;
;
(Ⅱ)当每件商品的售价为多少元时,该连锁分店一年的利润 最大,并求出
最大,并求出 的最大值.
的最大值.
已知函数 ,如果函数
,如果函数 恰有两个不同的极值点
恰有两个不同的极值点 ,
, ,且
,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)求 的最小值,并指出此时
的最小值,并指出此时 的值.
的值.