已知集合
，则集合
等于( )
A． |
B． |
C． |
D． |
( )
A． |
B． |
C． |
D． |
命题“
” 的否定是( )
A． |
B． |
C． |
D． |
已知
，则
( )
A． |
B． |
C． |
D． |
已知等差数列
的前
项和为
，
，
，取得最小值时
的值为( )
A． |
B． |
C． |
D． |
已知函数
是偶函数，且
则
( )
A． |
B． |
C． |
D． |
已知
则
( )
A． |
B． |
C． |
D． |
已知变量
满足约束条件
，则
的最大值为( )
A． |
B． |
C． |
D． |
角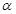
的终边经过点
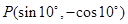，则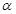的可能取值为( )
A． |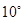
B． |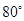
C． |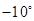
D． |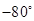
已知正数
满足
，则
的最小值为( )
A． |
B． |
C． |
D． |
函数
的图象为( )
已知函数
，若存在
，使得
，则
的取值范围为( )
A． |
B． |
C． |
D． |
____________.
公比为
的等比数列前
项和为15，前
项和为 .
不等式
的解集为_______________.
将函数
的图象上各点的纵坐标不变横坐标伸长到原来的2倍，再向左平移
个单位，所得函数的单调递增区间为 .
求值化简：
(Ⅰ)
；
(Ⅱ)
.
的角
的对边分别为
，已知
.
（Ⅰ）求角
；
（Ⅱ）若
，
,求
的值.
已知
为等差数列，且
.
（Ⅰ）求数列的通项公式及其前
项和
；
（Ⅱ）若数列
满足
求数列的通项公式.
已知函数
.
（Ⅰ）求
的最小正周期；
（Ⅱ）若
在
处取得最大值，求
的值;
（Ⅲ）求
的单调递增区间.
已知函数
.
（Ⅰ）若
，求
的极值；
（Ⅱ）若在定义域内无极值，求实数
的取值范围.
已知
，
为其反函数.
（Ⅰ）说明函数
与图象的关系（只写出结论即可）；
（Ⅱ）证明的图象恒在的图象的上方；
（Ⅲ）设直线
与、均相切，切点分别为（
）、（
），且
，求证：
.