已知全集
，
，
，那么
（ ）
A． |
B． |
C． |
D． |
在等比数列
中，
，则公比
等于（ ）
| A．2 | B． |
C．－2 | D． |
若函数
为偶函数，则
（ ）
A． |
B． |
C． |
D． |
“
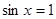”是“
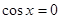”的（ ）
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
已知
，
，
，
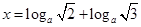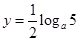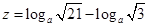，则（ ）
A． |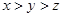
B． |
C． |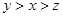
D． |
将函数
的图像向左平移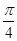
个单位，再向上平移1个单位，所得图像的函数解析式是（ ）
A． |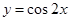
B． |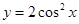
C． |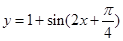
D． |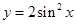
若函数
满足
,那么函数
的图象大致为（ ）
已知实数
，
，则
的最小值是（ ）
A． |
B． |
C． |
D． |
已知函数
，若
互不相等，且
，则
的取值范围是（ ）
A． |
B． |
C． |
D． |
已知数列
是等差数列，且
，则
的取值范围是（ ）
A． |
B． |
C． |
D． |
化简
的结果为 ；
已知平面向量
，
，且
，则
的值为 .
已知
为等差数列，
，
，则
.
已知
，则
的值为 .
若函数
在区间
内有极值，则实数
的取值范围是 .
已知正
边长等于
，点
在其外接圆上运动，则
的最大值是 .
函数
与函数
恒有两不同的交点，则
的取值范围是 .
已知集合
为函数
的定义域，集合
.
（Ⅰ）求集合、
；
（Ⅱ）若是的真子集，求实数
的取值范围.
在锐角
中，
，
（Ⅰ）求角
的大小；
（Ⅱ）当
时，求面积的最大值.
已知向量
，
（Ⅰ）当
时，求
的值；
（Ⅱ）求函数
在
上的值域.
已知数列
为等比数列，其前
项和为
，已知
，且
，
，
成等差，
（Ⅰ）求数列的通项公式；
（Ⅱ）已知
（
），记
，若
对于
恒成立，求实数
的取值范围.
已知函数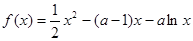
，
（Ⅰ）求函数
的单调区间；
（Ⅱ）若函数在区间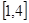
内的最小值为
，求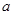
的值.（参考数据
）