下列运算正确的是( )
A.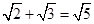 |
B.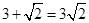 |
C.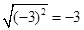 |
D.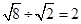 |
下列标志既是轴对称图形又是中心对称图形的是( )
A. |
B. |
C. |
D. |
已知实数a、b在数轴上的对应点的位置如右图所示,那么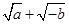 是一个( ).
是一个( ).
| A.非负数 | B.正数 | C.负数 | D.以上答案均不对 |
在根式①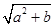 ②
②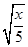 ③
③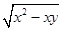 ④
④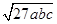 中最简二次根式是( )
中最简二次根式是( )
| A.①② | B.③④ | C.①③ | D.①④ |
在实数范围内定义运算“※”,其规则是a※b=a+b2,根据这个规则,方程x※(x+1)=5的解是( )
A.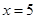 |
B.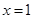 |
C.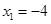 , ,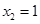 |
D.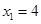 , ,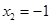 |
用配方法解关于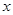 的一元二次方程
的一元二次方程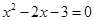 ,配方后的方程可以是( )
,配方后的方程可以是( )
A.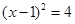 |
B. |
C.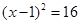 |
D.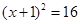 |
已知点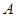 的坐标为
的坐标为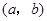 ,
,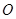 为坐标原点,连接
为坐标原点,连接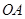 ,将线段
,将线段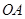 绕点
绕点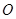 按逆时针方向旋转90°得线段
按逆时针方向旋转90°得线段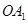 ,则点
,则点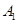 的坐标为( )
的坐标为( )
A.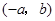 |
B.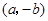 |
C.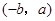 |
D.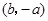 |
关于x的方程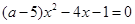 有实数根,则
有实数根,则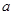 满足( )
满足( )
A.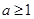 |
B.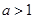 且 且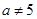 |
C.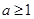 且 且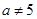 |
D.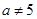 |
9月初,某蔬菜价格为10元/千克.由于部分菜农盲目扩大种植,至11月中旬,价格连续两次大幅下跌,现在价格为3元/千克.要求平均每次下跌的百分率 ,根据题意,下面所列方程正确的是( )
,根据题意,下面所列方程正确的是( )
A. |
B. |
C. |
D. |
已知:如图,在等边△ABC中取点P,使得PA、PB、PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°到线段AD,连接BD,下列结论:
①△ABD可以由△APC绕点A顺时针旋转60°得到;②点P与点D的距离为3; ③∠APB=150°;④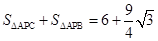
其中正确的结论有 ( )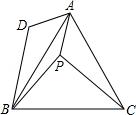
A.1个 B.2个 C.3个 D.4个
若 ,则
,则 _____
_____
若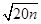 是整数,则正整数
是整数,则正整数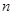 的最小值为_____.
的最小值为_____.
当代数式 的值等于7时,代数式
的值等于7时,代数式 的值是 .
的值是 .
如果关于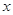 的方程
的方程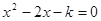 没有实数根,则
没有实数根,则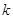 的取值范围为_____________.
的取值范围为_____________.
使 有意义的
有意义的 的取值范围是_______.
的取值范围是_______.
已知关于 的方程
的方程 的一个根为2,则
的一个根为2,则 =______.
=______.
如果 那么
那么 _______
_______
若 且
且 ,则一元二次方程
,则一元二次方程 必有一个定根,它是_______
必有一个定根,它是_______
已知关于 的方程:
的方程: ,是一元二次方程,则
,是一元二次方程,则 的值为_______.
的值为_______.
已知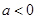 ,则点P(
,则点P( )关于原点的对称点P′在第_____象限
)关于原点的对称点P′在第_____象限
计算:
(1)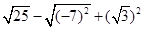
(2)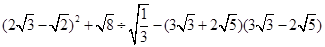
解方程:(1)
(2)
有一道练习题:对于式子 先化简,后求值,其中
先化简,后求值,其中 .小明的解法如下:
.小明的解法如下: =
= =
= =
= =
= .小明的解法对吗?如果不对,请改正.
.小明的解法对吗?如果不对,请改正.
在平面直角坐标系中,△ABC的顶点坐标是A(-7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,-1),E(-1,-7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市经市场调查发现,在进货价不变的情况下,若每千克涨价为1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使得顾客得到实惠,那么每千克应涨价多少元?
将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图①的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.
(1)求证:△BCE≌△B1CF.
(2)当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.