设全集U=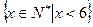 ,集合A={1,3},B={3,5},则
,集合A={1,3},B={3,5},则 ( )
( )
A.{0,4} |
B.{1,5} | C.{2,4} | D.{2,5} |
不等式 的解集为( )
的解集为( )
A. |
B.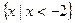 |
C.  |
D. |
已知 ,则
,则 ( )
( )
A. |
B. |
C. |
D.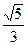 |
函数 是 ( )
是 ( )
A.最小正周期为2 的奇函数 的奇函数 |
B.最小正周期为2 的偶函数 的偶函数 |
C.最小正周期为 的奇函数 的奇函数 |
D.最小正周期为 的偶函数 的偶函数 |
记 ,那么
,那么 ( )
( )
A. |
B.- |
C. |
D.- ( ( |
函数y=1+ln(x-1)(x>1)的反函数是 ( )
| A.y=ex+1-1(x>0) | B.y=ex+1+1(x>0) |
| C.y="ex+1-1" (x∈R) | D.y="ex+1+1" (x∈R) |
已知各项均为正数的等比数列{ },
}, =5,
=5, =10,则
=10,则
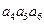 =( )
=( )
A. |
B.7 | C.6 | D. |
如果等差数列{an} 中,a3+a4+a5=12,那么a1+a2+……+ a7=( )
| A.14 | B.21 | C.28 | D.35 |
设a= 2,b=ln2,c=
2,b=ln2,c= ,则( )
,则( )
| A.a<b<c | B.b<c<a | C.c<a<b | D.c<b<a |
下列四类函数中,有性质“对任意的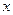 >0,
>0,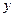 >0,函数
>0,函数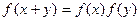 ”的是( )
”的是( )
| A.二次函数 | B.对数函数 | C.指数函数 | D.余弦函数 |
某学校要招开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数 与该班人数
与该班人数 之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( )
之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( )
A.y=[ ] ] |
B.y=[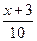 ] ] |
C.y=[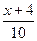 ] ] |
D.y=[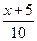 ] ] |
△ABC种,点D在边AB上,CD平分∠ACB,若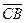 =a,
=a,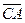 =b,|a|=1,|b|=2,则
=b,|a|=1,|b|=2,则 =( )
=( )
A.  |
B.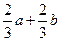 |
C. |
D. |
已知向量 =(2,-1),
=(2,-1), =(―1,
=(―1, ),
),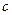 =(―1,2)若
=(―1,2)若 ,则
,则 =_________.
=_________.
若函数f(x)的反函数为f-1(x)=x2(x>0),则f(4)= ___________.
已知 为第三象限的角,
为第三象限的角, ,则
,则 .
.
已知函数
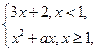 若
若 ,则实数
,则实数 _____________.
_____________.
已知α是第一象限的角,且cosα= 的值.
的值.
记函数f(x)=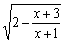 的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
(1)求A;
(2)若B A,求实数a的取值范围.
A,求实数a的取值范围.
(本小题共10分)
已知 为等差数列,且
为等差数列,且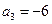 ,
, 。
。
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若等比数列 满足
满足 ,
, ,求
,求 的前n项和公式
的前n项和公式
(本小题共12分)
已知函数
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最大值和最小值
的最大值和最小值
(本小题满分12分)
已知{an}是各项均为正数的等比例数列,且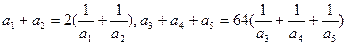
(Ⅰ)求{an}的通项公式;
(Ⅱ)设 ,求数列{bn}的前N项和Tn。
,求数列{bn}的前N项和Tn。
已知数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(n≥2,q≠0).
(1)设bn=an+1-an(n∈N*),证明{bn}是等比数列; (2)求数列{an}的通项公式;
(3)若a3是a6与a9的等差中项,求q的值,并证明:对任意的n∈N*,an是an+3与an+6的等差中项.