下列四组数中,能组成比例的是( ).
A. , , , , , , ; ; |
B. , , , , , , ; ; |
C. , , , , , , ; ; |
D. , , , , , , . . |
在比例尺为 的地图上测得
的地图上测得 、
、 两地间的图上距离为
两地间的图上距离为 ,则
,则 两地间的实际距离为( ).
两地间的实际距离为( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
已知在 中,
中, ,
, ,
, ,那么
,那么 的长为( ).
的长为( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
如图,点 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 都是
都是 方格纸(每个小方格均为正方形)中的格点,为使△
方格纸(每个小方格均为正方形)中的格点,为使△ ∽△
∽△ ,则点
,则点 应是
应是 、
、 、
、 、
、 四点中的( ).
四点中的( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
如图,在△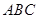 中,点D、E分别在边AB 、AC上,下列比例式不能判定
中,点D、E分别在边AB 、AC上,下列比例式不能判定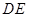 ∥
∥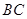 的是( ).
的是( ).
A.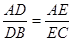 ; B.
; B.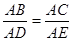 ;C.
;C.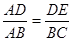 ;D.
;D.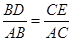 .
.
已知△ ,
, ,
, ,
, 分别是
分别是 ,
, ,
, 的中点,设
的中点,设 ,
, ,则
,则 是( ).
是( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
若 ,则
,则 .
.
若两个相似三角形的面积之比为 ,则在这两个三角形中,面积较小的三角形与面积较大的三角形的周长之比为 .
,则在这两个三角形中,面积较小的三角形与面积较大的三角形的周长之比为 .
如图, ∥
∥ ,
, ,则
,则 .
.
在△ 中,
中, ,如果
,如果 ,
, ,那么
,那么 .
.
已知线段 ,延长
,延长 到点
到点 ,使
,使 ,则
,则
 .
.
已知点 是线段
是线段 的黄金分割点,
的黄金分割点, >
> ,且
,且 ,则
,则 .
.
如图,在△ABC中,AD是中线,G是重心,过点G作EF∥BC,分别交AB、AC于点 、
、 ,若
,若 ,则
,则 .
.
如图,已知直线 ∥
∥ ∥
∥ ,
, ,
, ,
, ,则
,则 .
.
如图,在 中,点
中,点 、
、 分别在边
分别在边 、
、 上,
上, 平分
平分 ,
, ,如果
,如果 ,
, ,那么
,那么 .
.
.如图,正方形 内接于△
内接于△ ,已知
,已知 ,
, ,那么正方形的边长是 .
,那么正方形的边长是 .
已知 的两条直角边之比为
的两条直角边之比为 ,△
,△ ∽△
∽△ ,若△
,若△ 的最短边长
的最短边长 ,则△
,则△ 最长边的中线长为
最长边的中线长为  .
.
在△ 中,
中, ,
, ,
, ,延长
,延长 至点
至点 ,使
,使 ,则
,则 .
.
计算:
如图,在 △
△ 中,
中, ,
, ,
, .
.
(1)求 的长;(2)求
的长;(2)求 的值.
的值.
如图,已知向量 、
、 ,求作向量
,求作向量 ,使
,使 满足
满足 (不要求写作法,但要保留作图痕迹,并写结论)
(不要求写作法,但要保留作图痕迹,并写结论)
已知:如图,△ 是等边三角形,点
是等边三角形,点 、
、 分别在边
分别在边 、
、 上,
上, .
.
(1)求证:△ ∽△
∽△ ;(2)如果
;(2)如果 ,
, ,求
,求 的长.
的长.
如图,在△ 中,
中, ,
, ,作
,作 ,垂足为
,垂足为 ,
, 为边
为边 上一点,联结
上一点,联结 交
交 于点
于点 ,点
,点 为线段
为线段 上一点,且
上一点,且 ,联结
,联结 .
.
(1)求证: ∥
∥ ;(2)当
;(2)当 ,且
,且 时,求
时,求 的长.
的长.
如图:已知一次函数 的图像分别交
的图像分别交 轴、
轴、 轴于
轴于 、
、 两点,且点
两点,且点 在一次函数
在一次函数 的图像上,
的图像上, ⊥
⊥ 轴于点
轴于点 .
.
(1)求 的值及
的值及 、
、 两点的坐标;
两点的坐标;
(2)如果点 在线段
在线段 上,且
上,且 ,求
,求 点的坐标;
点的坐标;
(3)如果点 在
在 轴上,那么当△
轴上,那么当△ 与△
与△ 相似时,求点
相似时,求点 的坐标.
的坐标.
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE ,CF
,CF .
.
图1
(1)求 关于
关于 的函数解析式,并写出
的函数解析式,并写出 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: ;
;
图2
(3)在(2)的条件下,当 时,求
时,求 的值.
的值.