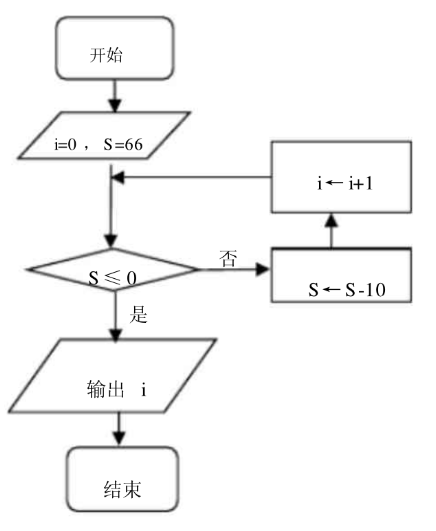
函数
的定义域为
若集合
,则
=.
在
中,
,则
=
若行列式
,则
.
若
,则
.(结果用反三角函数表示)
两条直线
与
的夹角的大小是.
若
为等比数列
的前
项的和,
,则
=.
若椭圆
的焦点和顶点分别是双曲线
的顶点和焦点,则椭圆
的方程是.
若点
和点
分别为椭圆
的中心和左焦点,点
为椭圆上的任意一点,则
的最小值为.
2011年上海春季高考有8所高校招生,如果某3位同学恰好被其中2所高校录取,那么录取方法的种数为.
有一中多面体的饰品,其表面右6个正方形和8各正三角形组成(如图),
与
所成的角的大小是.

为求方程
的虚根,可以把原方程变形为
,由此可得原方程的一个虚根为.
若向量
,则谢列结论正确的是()
| A. |
|
B. |
. |
C. |
|
D. |
|
的图像关于( )
| A. |
原点对称 |
B. |
直线
对称 |
C. |
直线
对称 |
D. |
轴对称 |
直线
与圆
的位置关系是 ( )
| A. |
相交或相切 |
B. |
相交或相离. |
C. |
相切. |
D. |
相交 |
若
均为单位向量,则
是
的
| A. |
充分不必要条件. |
B. |
必要不充分条件. |
| C. |
充要条件. |
D. |
既不充分也不必要条件 |
已知向量
,设函数
,求函数
的最小正周期及
时的最大值.
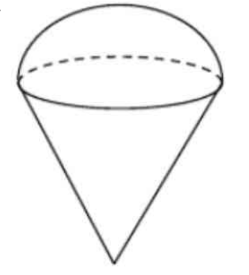
某甜品店制作蛋筒冰淇淋,其上半部分呈半球形,下半部分呈圆锥形(如图)。现把半径为10cm的圆形蛋皮分成5个扇形,用一个扇形蛋皮围成锥形侧面(蛋皮厚度忽略不计),求该蛋筒冰淇淋的表面积和体积(精确到0.01)
已知抛物线
(1)
的三个顶点在抛物线
上,记
的三边
、
、
所在的直线的斜率分别为
,
,
若A的坐标在原点,求
的值;
(2)请你给出一个以
为顶点、其余各顶点均为抛物线
上的动点的多边形,写出各多边形各边所在的直线斜率之间的关系式,并说明理由
定义域为
,且对任意实数
都满足不等式
的所有函数
组成的集合记为
,例如,函数
.
(1)已知函数
,证明:
;
(2)写出一个函数
,使得
,并说明理由;
(3)写出一个函数
,使得数列极限
.
对于给定首项
,由递推公式
得到数列
,对于任意的
,都有
,用数列
可以计算
.
(1)取
,计算
的值(精确到0.01);归纳出
的大小关系;
(2)当
时,证明:
.
(3)当
时,用数列
计算
的近似值,要求
,请你估计
,并说明理由