如果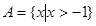 ,那么..( )
,那么..( )
A. |
B.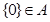 |
C.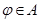 |
D.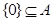 |
已知集合 ,则A∩B=( )
,则A∩B=( )
A. |
B. |
C. |
D. |
如果 ,那么
,那么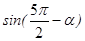 等于( )
等于( )
A.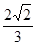 |
B. |
C. |
D.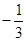 |
已知函数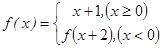 ,则
,则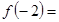 ( )
( )
| A.0 | B.1 | C.-2 | D.-1 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. |
B.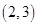 |
C. |
D. |
下列函数中,周期为 的是.( )
的是.( )
A. |
B. |
C. |
D.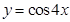 |
设偶函数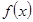 的定义域为R,当
的定义域为R,当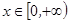 时
时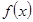 是增函数,则
是增函数,则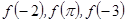 的大小关系是..( )
的大小关系是..( )
A.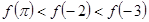 |
B.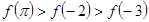 |
C.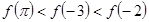 |
D.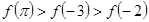 |
若函数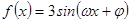 对任意的
对任意的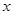 都有
都有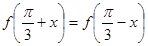 ,则
,则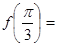 ( )
( )
A.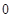 |
B.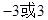 |
C.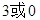 |
D.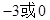 |
若函数 满足对任意的
满足对任意的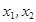 ,当
,当 时
时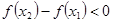 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数 的三个实数根分别为
的三个实数根分别为 ,则
,则 的范围是( )
的范围是( )
A. |
B. |
C. |
D. |
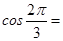 ___________;
___________;
函数 的定义域为____________;
的定义域为____________;
函数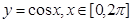 的图象和直线
的图象和直线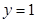 围成一个封闭的平面图形,这个封闭图形的面积是_____________;
围成一个封闭的平面图形,这个封闭图形的面积是_____________;
函数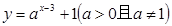 恒过定点_____________;
恒过定点_____________;
已知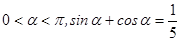 ,则
,则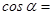 ________________;
________________;
已知函数 是定义在R上的奇函数,且
是定义在R上的奇函数,且  在
在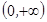 单调递增,若
单调递增,若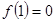 ,则不等式
,则不等式 的解集是 ___________
的解集是 ___________
关于函数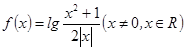 ,有下列命题:①函数
,有下列命题:①函数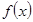 的图象关于
的图象关于 轴对称;②函数
轴对称;②函数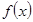 的图象关于
的图象关于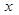 轴对称;③函数
轴对称;③函数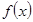 的最小值是0;④函数
的最小值是0;④函数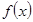 没有最大值;⑤函数
没有最大值;⑤函数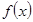 在
在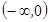 上是减函数,在
上是减函数,在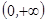 上是增函数。其中正确命题的序号是___________________。
上是增函数。其中正确命题的序号是___________________。
已知集合 ,集合
,集合 .
.
(1)求 ,
, ;
;
(2)设 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
已知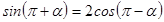 ,计算:
,计算:
(1)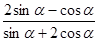 ;
;
(2)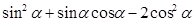 .
.
计算:
(2)已知函数 ,求它的定义域和值域。
,求它的定义域和值域。
设函数 。
。
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)求函数 在区间
在区间 上的最小值和最大值,并求出取最值时
上的最小值和最大值,并求出取最值时 的值。
的值。
已知 ,
, ,
,
(1)求函数 的解析式,并求它的单调递增区间;
的解析式,并求它的单调递增区间;
(2)若 有四个不相等的实数根,求
有四个不相等的实数根,求 的取值范围。
的取值范围。