已知集合
，
，则
（ ）
A． |
B． |
C． |
D． |
下列函数中，既是偶函数又在区间
上是单调递减函数的是（ ）
A． |
B． |
C． |
D． |
设
是虚数单位，若复数
是实数，则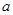
的值为（ ）
A． |
B． |
C． |
D． |
等差数列
中，
，
，则此数列前
项和等于（ ）
A． |
B． |
C． |
D． |
已知向量
，
，若
，则实数
（ ）.
A． 或 |
B． |
C． |
D． |
若点
位于曲线
与
所围成的封闭区域，则
的最小值为（ ）
A． |
B． |
C． |
D． |
将函数
的图像向右平移
个单位长度后，所得到的图像关于
轴对称，则
的最小值为（ ）
A． |
B． |
C． |
D． |
椭圆
的离心率大于
的充分必要条件是（ ）
A． |
B． |
C． |
D． 或 |
阅读如图所示的程序框图，运行相应的程序.若输入
的值为
，则输出的结果为
（ ）
A． |
B． |
C． |
D． |
给出下列关于互不相同的直线
和平面
的四个命题：
①若
，
，点
，则
与
不共面；
②若、是异面直线，
，
，且
，
，则
；
③若
，则
；
④若
，，
，
，
，则
.
其中为假命题的是（ ）
| A．① | B．② | C．④ | D．③ |
下图中的三个直角三角形是一个体积为
的几何体的三视图，则
.
据统计，高三年级男生人数占该年级学生人数
.在上次考试中，男、女生数学平均分数分别为
、
，则这次考试该年级学生平均分数为_________.
设常数
，若
对一切正实数
成立，则
的取值范围为_________.
如图，在
中，
，
圆
经过
、
，且与
、
分别相交于、
.若
，则圆的半径
________.
在平面直角坐标系中，直线
的参数方程为
（参数
），圆的参数方程为
（参数
），则圆心到直线的距离为_______.
已知函数
，
.
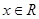（1）当
为何值时，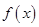
取得最大值，并求出其最大值；
（2）若
，
，求
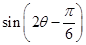的值.
随着工业化的发展，环境污染愈来愈严重.某市环保部门随机抽取60名市民对本市空气质量满意度打分，把数据分
、
、
、
六段后得到如下频率分布表：
| 分组 |
频数 |
频率 |
|
 |
 |
|
 |
 |
 |
|
|
 |
 |
 |
 |
 |
 |
|
 |
 |
| 合计 |
 |
 |
（1）求表中数据、、的值；
（2）用分层抽样的方法在分数
的市民中抽取容量为的样本，将该样本看成一个总体，从中任取
人在分数段的概率.
在如图的多面体中，
平面
，
，
，
，
，
，
，
是
的中点.
（1）求证：
平面
；
（2）求证：
；
（3）求三棱锥
的体积.
设数列
的前
项和为
，且
.
（1）求数列的通项公式；
（2）设
，求证：
.
已知点
直线
，
为平面上的动点，过点作直线
的垂线，垂足为
，且
.
（1）求动点的轨迹方程；
（2）
、
是轨迹
上异于坐标原点
的不同两点，轨迹在点、处的切线分别为
、
，且
，、相交于点
，求点的纵坐标.
已知函数
.
（1）若曲线
在
和
处的切线相互平行，求
的值；
（2）试讨论的单调性；
（3）设
，对任意的
，均存在
，使得
.试求实数的取值范围.