已知全集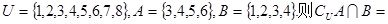 ( )
( )
A.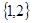 |
B.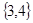 |
C.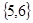 |
D.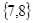 |
在直角坐标系中,已知点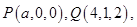 且
且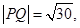 则
则 ( )
( )
| A.1 | B. -1 | C.-1或9 | D.1或9 |
设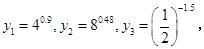 则( )
则( )
A.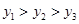 |
B.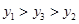 |
C.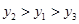 |
D.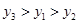 |
过点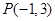 且垂直于直线
且垂直于直线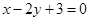 的直线方程为( )
的直线方程为( )
A.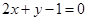 |
B.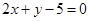 |
C.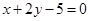 |
D.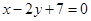 |
已知过点 和
和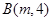 的直线与直线
的直线与直线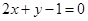 平行,则
平行,则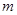 的值为( )
的值为( )
| A.0 | B.-8 | C.2 | D.10 |
直线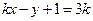 ,当
,当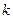 变动时,所有直线都通过定点( )
变动时,所有直线都通过定点( )
A.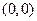 |
B. |
C.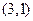 |
D.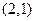 |
若直线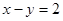 被圆
被圆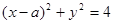 所截得的弦长为
所截得的弦长为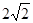 ,则实数
,则实数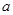 的值为( )
的值为( )
A.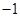 或 或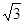 |
B.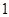 或 或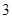 |
C.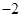 或 或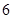 |
D.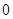 或 或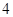 |
如果一个水平放置的图形的斜二测直观图是一个底角为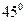 ,腰和上底均为
,腰和上底均为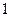 的等腰梯形,那么原平面图形的面积是( )
的等腰梯形,那么原平面图形的面积是( )
A.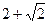 |
B.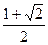 |
C.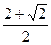 |
D.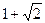 |
若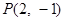 为圆
为圆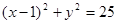 的弦
的弦 的中点,则直线
的中点,则直线 的方程是( )
的方程是( )
A.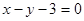 |
B.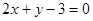 |
C.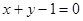 |
D.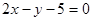 |
如图,在多面体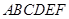 中,已知平面
中,已知平面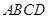 是边长为
是边长为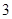 的正方形,
的正方形,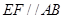 ,
,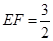 ,且
,且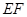 与平面
与平面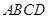 的距离为
的距离为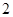 ,则该多面体的体积为( )
,则该多面体的体积为( )
A.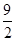 |
B.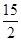 |
C.5 | D.6 |
函数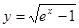 的定义域为
的定义域为
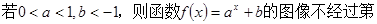 象限.
象限.
若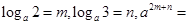
如右图为长方体积木块堆成的几何体的三视图,此几何
体共由 块木块堆成
点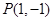 到直线
到直线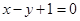 的距离是_______.
的距离是_______.
(本小题共12分)对于二次函数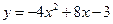 ,
,
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)求函数的最大值或最小值;
(3)分析函数的单调性。
(本小题共12分) 证明函数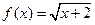 在
在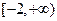 上是增函数。
上是增函数。
(本小题共12分) 已知两圆 ,
,
求(1)它们的公共弦所在直线的方程;(2)公共弦长。
(本小题共12分)北京奥运会纪念章某特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向北京奥组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为x元(x∈N*).(Ⅰ)写出该特许专营店一年内销售这种纪念章所获得的利润y(元)与每枚纪念章的销售价格x的函数关系式(并写出这个函数的定义域);(Ⅱ)当每枚纪念销售价格x为多少元时,该特许专营店一年内利润y(元)最大,并求出这个最大值.
(本小题共13分)直线 和
和 轴,
轴, 轴分别交于点
轴分别交于点 ,以线段
,以线段 为边在第一象限内作等边△
为边在第一象限内作等边△ ,如果在第一象限内有一点
,如果在第一象限内有一点 使得△
使得△ 和△
和△ 的面积相等, 求
的面积相等, 求 的值。
的值。
(本小题共14分)
如图,四棱锥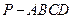 的底面是正方形,
的底面是正方形,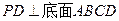 ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面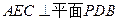 ;
;
(Ⅱ)当 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.