已知集合 则
则 ( )
( )
A. |
B. |
C. |
D. |
已知命题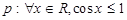 ,则( )
,则( )
A.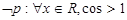 |
B.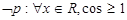 |
C.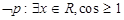 |
D.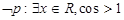 |
已知复数 (其中
(其中 为虚数单位),则复数
为虚数单位),则复数 在复平面内对应的点在( )
在复平面内对应的点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
在各项都为正数的等比数列 中,首项为3,前3项和为21,则
中,首项为3,前3项和为21,则 等于( )
等于( )
| A.15 | B.12 | C.9 | D.6 |
下列函数中既是偶函数,又在区间 上单调递增的函数是( )
上单调递增的函数是( )
A. |
B. |
C. |
D. |
已知向量
 ,
,
 ,且
,且 ,则
,则 的值为 ( )
的值为 ( )
A. |
B. |
C. |
D. |
若 ,且
,且 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知 ,则下列不等式中总成立的是( )
,则下列不等式中总成立的是( )
A. |
B. |
C. |
D. |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向右平移 个单位长度 个单位长度 |
如图,已知 用
用 表示
表示 ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
已知函数 的图象如右图所示,则
的图象如右图所示,则 的解析式可以是 ( )
的解析式可以是 ( )
A. |
B. |
C. |
D. |
已知定义域为 的函数
的函数 满足
满足 ,且对任意
,且对任意 总有
总有 ,则不等式
,则不等式 的解集为 ( )
的解集为 ( )
A. |
B. |
C. |
D. |
等差数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值是 .
的值是 .
已知实数 满足约束条件
满足约束条件 ,则
,则 的最小值是 .
的最小值是 .
已知集合 ,
, .若
.若 ,则
,则 的取值范围是 .
的取值范围是 .
将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为 .
已知等差数列 中,
中, .
.
(I)求数列 的通项公式;
的通项公式;
(II)若数列 的前
的前 项和
项和 ,求
,求 的值.
的值.
设函数 (
( ),其中
),其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的极大值和极小值.
的极大值和极小值.
已知函数 的图象的一部分如下图所示.
的图象的一部分如下图所示.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)当 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 且
且 构成等比数列.
构成等比数列.
(Ⅰ)证明: ;
;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)证明:对一切正整数 ,有
,有 .
.
如图,甲船以每小时 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
已知 ,
, ,
, ,
, .
.
(Ⅰ)请写出的 表达式(不需证明);
表达式(不需证明);
(Ⅱ)求 的极小值
的极小值 ;
;
(Ⅲ)设 ,
, 的最大值为
的最大值为 ,
, 的最小值为
的最小值为 ,试求
,试求 的最小值.
的最小值.