若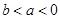 ,则下列结论不正确的是
,则下列结论不正确的是
| A.a2<b2 | B.ab<b2 | C. |
D.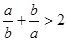 |
不等式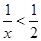 的解集是
的解集是
A.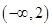 |
B.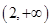 |
C.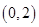 |
D.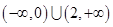 |
已知 ,
, ,且
,且 ,则
,则
A. |
B. |
C. |
D. |
已知锐角 的面积为
的面积为 ,
, ,则角
,则角 的大小为
的大小为
| A.75° | B.60° | C.45° | D.30° |
已知 ,
, 为实数,则
为实数,则 是
是 的
的
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在平面直角坐标系 中,已知
中,已知 顶点
顶点 和
和 ,顶点
,顶点 在椭圆
在椭圆 上,则
上,则 的值是
的值是
| A.0 | B.1 | C.2 | D.不确定 |
在各项都为正数的等比数列 中,首项
中,首项 ,前三项和为
,前三项和为 ,则
,则 =
=
A. |
B. |
C. |
D. |
已知抛物线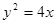 的焦点为F,准线与x轴的交点为M,N为抛物线上的一点, 且
的焦点为F,准线与x轴的交点为M,N为抛物线上的一点, 且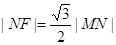 ,则
,则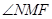 =
=
A.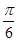 |
B.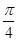 |
C.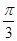 |
D.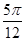 |
函数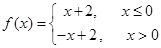 ,则不等式
,则不等式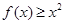 的解集是
的解集是
A.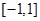 |
B.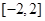 |
C.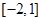 |
D.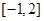 |
已知双曲线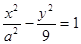
 的中心在原点, 右焦点与抛物线
的中心在原点, 右焦点与抛物线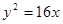 的焦点重合,则该双曲线的离心率等于
的焦点重合,则该双曲线的离心率等于
A.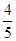 |
B.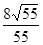 |
C.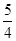 |
D.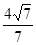 |
已知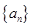 为等差数列,
为等差数列,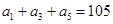 ,
,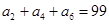 ,
,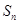 是等差数列
是等差数列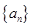 的前
的前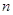 项和,则使得
项和,则使得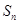 达到最大值的
达到最大值的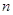 是
是
| A.21 | B.20 | C.19 | D.18 |
椭圆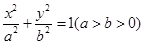 的右焦点
的右焦点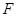 ,直线
,直线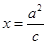 与
与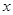 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点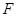 ,则椭圆离心率的取值范围是
,则椭圆离心率的取值范围是
A.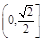 |
B.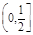 |
C.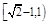 |
D.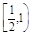 |
以椭圆 的顶点为焦点,以椭圆的焦点为顶点的双曲线方程为
的顶点为焦点,以椭圆的焦点为顶点的双曲线方程为
已知实数 ,满足约束条件
,满足约束条件 则
则 的最小值为
的最小值为
已知向量 =(2,4,x),
=(2,4,x), =(2,y,2),若|
=(2,y,2),若| |=6,
|=6, ⊥
⊥ ,则x+y的值是
,则x+y的值是
正项的等差数列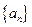 中,
中,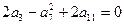 ,数列
,数列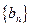 是等比数列,且
是等比数列,且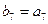 ,则
,则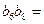 ____
____
(本小题满分10分)
已知 ,命题
,命题 函数
函数 在
在 上单调递减,命题
上单调递减,命题 曲线
曲线
 与
与 轴交于不同的两点,若
轴交于不同的两点,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。
(本小题满分12分)
已知△ABC中,内角A,B,C的对边分别为a,b,c,已知a,b,c成等比数列, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 的值。
的值。
如图,在直三棱柱 中,
中, ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 ⊥平面
⊥平面 ?若存在,找出点
?若存在,找出点 的位置幷证明;若不存在,请说明理由;
的位置幷证明;若不存在,请说明理由;
(Ⅱ)求平面 和平面
和平面 所成角的大小
所成角的大小
如图所示,某公园预计在一块绿地的中央修建两个相同的矩形的池塘,每个面积为10000米2,池塘前方要 留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?
留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?
(本小题满分12分)
设数列 的前
的前 项和为
项和为 ,且
,且 数列
数列 满足
满足 ,点
,点 在直线
在直线 上,
上, .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
已知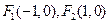 ,点
,点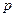 满足
满足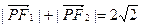 ,记点
,记点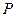 的轨迹
的轨迹 为
为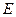 .
.
(Ⅰ)求轨迹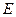 的方程;
的方程;
(Ⅱ)过点F2(1 ,0)作直线l与轨迹
,0)作直线l与轨迹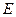 交于不同的两点A、B,设
交于不同的两点A、B,设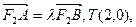
 ,若
,若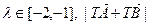 的取值范围
的取值范围