在等差数列 中,若
中,若 ,则
,则 的前
的前 项和
项和
A. |
B. |
C. |
D. |
已知 ,那么下列不等式成立的是
,那么下列不等式成立的是
A. |
B. |
C. |
D. |
 的值为
的值为
A. |
B. |
C. |
D. . . |
若变量 满足约束条件
满足约束条件 ,则
,则 的最大值为 ( )
的最大值为 ( )
A. |
B. |
C. |
D. |
下列说法错误的是 ( )
| A.命题“若x2—4x+3=0,则x=3”的逆否命题是“若x≠3,则x2-4x+3≠0” |
| B.“x>l”是“|x|>0”的充分不必要条件 |
| C.若p∧q为假命题,则p、g均为假命题 |
D.命题P:“ ,使得x2+x+1<0”,则 ,使得x2+x+1<0”,则  |
向量 ,
, ,且
,且 ,则锐角
,则锐角 的余弦值为( )
的余弦值为( )
A. |
B. |
C. |
D. |
已知函数 是
是 上的减函数,那么实数
上的减函数,那么实数 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.(0,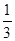 ) ) |
C.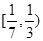 |
D.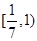 |
若 ,则f(2016)等于 ( )
,则f(2016)等于 ( )
| A.0 | B. |
C. |
D. |
函数 (其中A>0,
(其中A>0, )的图象如图所示,为得到
)的图象如图所示,为得到 的图象,则只要将
的图象,则只要将 的图象( )
的图象( )
A.向右平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
已知函数f(x)在R上满足 ,则曲线y=f(x)在点 (1,f(1))处切线的斜率是 ( )
,则曲线y=f(x)在点 (1,f(1))处切线的斜率是 ( )
| A.2 | B.1 | C.3 | D.-2 |
已知圆的方程为 ,直线l的方程为
,直线l的方程为 ,若圆与直线相切,则实数m= .
,若圆与直线相切,则实数m= .
数列 的前
的前 项和为
项和为 ,且
,且 ,则
,则 的通项公式
的通项公式 _____.
_____.
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+m,则f(﹣1)= .
如图,半径为 的圆
的圆 中,
中, ,
, 为
为 的中点,
的中点, 的延长线交圆
的延长线交圆 于点
于点 ,则线段
,则线段 的长为 .
的长为 .
在极坐标系中,已知两点A、B的极坐标分别为(3, ),(4,
),(4, ),则△AOB(其中O为极点)的面积为 .
),则△AOB(其中O为极点)的面积为 .
在实数范围内,不等式 的解集为 .
的解集为 .
已知 ,且A=
,且A= ,
, ,求
,求 和
和 .
.
已知函数 .
.
(Ⅰ)求 的单调减区间;
的单调减区间;
(Ⅱ)求 在区间
在区间 上最大值和最小值.
上最大值和最小值.
已知函数 ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴.
轴.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的极值.
的极值.
在 中,三个内角
中,三个内角 所对边的长分别为
所对边的长分别为 ,已知
,已知 .
.
(Ⅰ)判断 的形状;
的形状;
(Ⅱ)设向量 ,若
,若 ,求
,求 .
.
已知函数 .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
设数列{an} 的前n项和为Sn,满足2Sn=an+1﹣2n+1+1,n∈N*,且a1,a2+5,a3成等差数列.
(1)求a1,a2,a3的值;
(2)求证:数列{an+2n}是等比数列;
(3)证明:对一切正整数n,有 +
+ +…+
+…+ <
< .
.