已知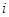 是虚数单位,则复数
是虚数单位,则复数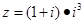 的共轭复数是( )
的共轭复数是( )
A.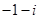 |
B.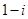 |
C.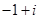 |
D.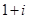 |
集合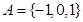 ,
,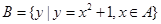 ,则
,则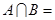 ( )
( )
A.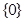 |
B.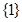 |
C.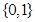 |
D.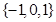 |
设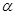 表示直线
表示直线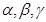 表示不同的平面,则下列命题中正确的是( )
表示不同的平面,则下列命题中正确的是( )
A.若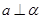 且 且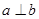 ,则 ,则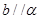 |
B.若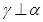 且 且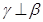 ,则 ,则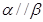 |
C.若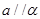 且 且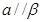 ,则 ,则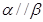 |
D.若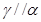 且 且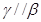 ,则 ,则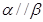 |
若抛物线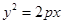 上一点
上一点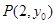 到其准线的距离为4,则抛物线的标准方程为( )
到其准线的距离为4,则抛物线的标准方程为( )
A.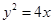 |
B.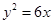 |
C.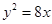 |
D.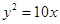 |
某程序框图如图所示,该程序运行后输出的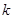 的值是( )
的值是( )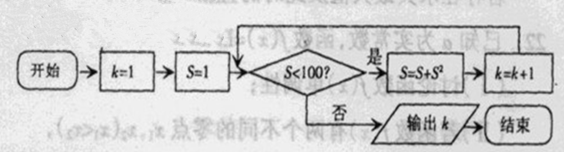
| A.4 | B.5 | C.6 | D.7 |
把边长为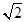 的正方形
的正方形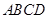 沿对角线
沿对角线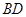 折起,连结
折起,连结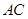 ,得到三棱锥
,得到三棱锥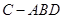 ,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )
,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )
A. |
B.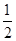 |
C.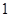 |
D.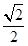 |
设变量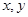 满足约束条件:
满足约束条件: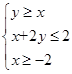 ,则
,则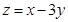 的最小值( )
的最小值( )
A.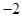 |
B.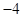 |
C.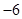 |
D.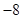 |
若双曲线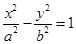
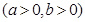 右顶点为
右顶点为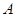 ,过其左焦点
,过其左焦点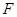 作
作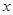 轴的垂线交双曲线于
轴的垂线交双曲线于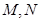 两点,且
两点,且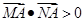 ,则该双曲线离心率的取值范围为( )
,则该双曲线离心率的取值范围为( )
A.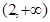 |
B.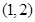 |
C.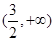 |
D.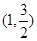 |
函数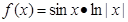 的部分图像为( )
的部分图像为( )
已知球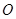 ,过其球面上
,过其球面上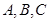 三点作截面,若
三点作截面,若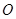 点到该截面的距离是球半径的一半,且
点到该截面的距离是球半径的一半,且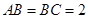 ,
,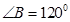 ,则球
,则球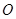 的表面积为( )
的表面积为( )
A. |
B.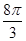 |
C.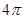 |
D.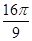 |
已知各项均为正数的等比数列 中,
中,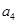 与
与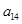 的等比中项为
的等比中项为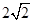 ,则
,则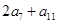 的最小值为( )
的最小值为( )
| A.16 | B.8 | C.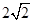 |
D.4 |
已知函数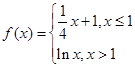 ,则方程
,则方程 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数 的取值范围是( )(注:
的取值范围是( )(注: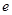 为自然对数的底数)
为自然对数的底数)
A.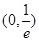 |
B.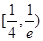 |
C.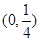 |
D.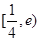 |
某学校共有师生3200人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 .
在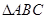 中,内角
中,内角 的对边长分别是
的对边长分别是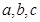 ,若
,若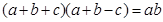 ,则角
,则角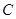 的大小为
的大小为
边长为1的菱形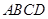 中,
中, ,
,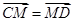 ,
,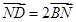 ,则
,则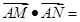 .
.
如图,一个类似杨辉三角的数阵,则第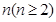 行的第2个数为 .
行的第2个数为 .
已知函数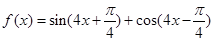 .
.
(1)求函数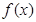 的最大值;
的最大值;
(2)若直线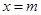 是函数
是函数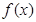 的对称轴,求实数
的对称轴,求实数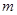 的值.
的值.
已知公差不为0的等差数列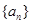 的前n项和为
的前n项和为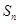 ,
,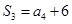 ,且
,且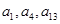 成等比数列.
成等比数列.
(1)求数列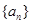 的通项公式;
的通项公式;
(2)设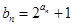 ,求数列
,求数列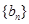 的前n项和.
的前n项和.
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在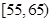 ,
,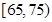 的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率.
的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率. 
如图,四棱锥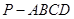 中,底面
中,底面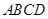 是边长为1的正方形,
是边长为1的正方形,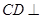 平面
平面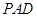 ,
, 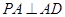 ,
,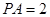 ,
,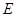 为
为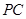 的中点,
的中点,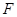 在棱
在棱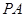 上.
上.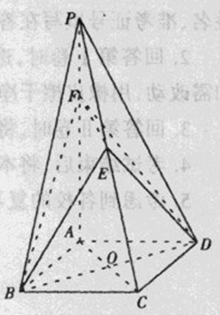
(1)求证: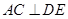 ;
;
(2)求三棱锥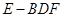 的体积.
的体积.
已知函数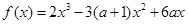
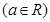 .
.
(1)当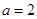 时,求函数
时,求函数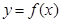 的单调区间;
的单调区间;
(2)若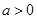 时,函数
时,函数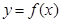 在闭区间
在闭区间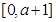 上的最大值为
上的最大值为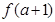 ,求
,求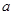 的取值范围.
的取值范围.
已知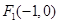 、
、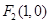 为椭圆
为椭圆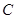 的左、右焦点,且点
的左、右焦点,且点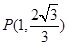 在椭圆
在椭圆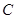 上.
上.
(1)求椭圆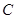 的方程;
的方程;
(2)过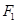 的直线
的直线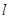 交椭圆
交椭圆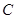 于
于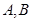 两点,则
两点,则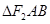 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值?
若存在其最大值及此时的直线方程;若不存在,请说明理由.