对于实数 ,“
,“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
在 中,
中, ,
, ,
, ,则
,则 面积为
面积为
A. |
B. |
C. 或 或 |
D. 或 或 |
设抛物线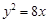 上一点
上一点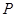 到直线
到直线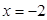 的距离是
的距离是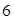 ,则点
,则点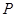 到该抛物线焦点的距离是
到该抛物线焦点的距离是
| A.12 | B.8 | C.6 | D.4 |
设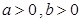 且
且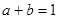 则
则 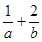 的最小值是
的最小值是
A.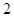 |
B.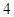 |
C.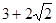 |
D.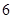 |
若规定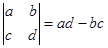 则不等式
则不等式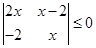 的解集是
的解集是
A.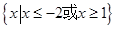 |
B.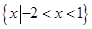 |
C.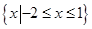 |
D.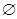 |
若椭圆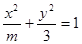 的右焦点与抛物线
的右焦点与抛物线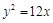 的焦点重合,则
的焦点重合,则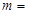
| A.3 | B.6 | C.9 | D.12 |
设等差数列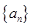 的前
的前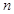 项和为
项和为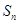 ,若
,若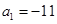 ,
,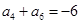 ,则当
,则当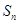 取最小值时,
取最小值时,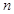 等于
等于
| A.6 | B.7 | C.8 | D.9 |
若数列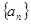 的通项公式为
的通项公式为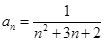 ,其前
,其前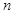 项和为
项和为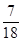 ,则
,则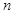 为
为
| A.5 | B.6 | C.7 | D.8 |
在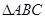 中,角
中,角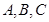 所对的边长分别为
所对的边长分别为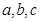 ,若
,若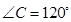 ,
,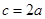 ,则
,则
A.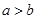 |
B.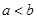 |
C.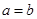 |
D.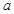 与 与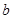 的大小关系不能确定 的大小关系不能确定 |
设双曲线的一个焦点为 ,虚轴的一个端点为
,虚轴的一个端点为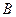 ,如果直线
,如果直线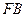 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
A.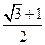 |
B.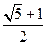 |
C.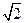 |
D.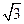 |
已知命题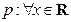 ,
,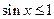 ,则
,则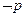 是
是  .
.
在等比数列 中,
中, ,则
,则 .
.
甲船在A处观察到乙船在它的北偏东 的方向,两船相距
的方向,两船相距 海里,乙船正在向北行驶,若甲船的速度是乙船的
海里,乙船正在向北行驶,若甲船的速度是乙船的 倍,则甲船应取北偏东
倍,则甲船应取北偏东 方向前进,才能尽快追上乙船,此时
方向前进,才能尽快追上乙船,此时 .
.
过点 的动直线
的动直线 与
与 轴的交点分别为
轴的交点分别为 ,过
,过 分别作
分别作 轴的垂线,则两垂线交点
轴的垂线,则两垂线交点 的轨迹方程为: .
的轨迹方程为: .
(本小题满分12分)
已知命题 :关于
:关于 的方程
的方程 有实数解,命题
有实数解,命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 ,若
,若 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)
在 中,角
中,角 所对的边长分别为
所对的边长分别为 ,
, ,
,  ,
,  , (1)求
, (1)求 的值; (2)求
的值; (2)求 的值.
的值.
(本小题共14分)
某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、
B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如下表: 如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
(本小题满分14分)
已知直角梯形 中(如图1),
中(如图1), ,
, 为
为 的中点,
的中点,
将 沿
沿 折起,使面
折起,使面 面
面 (如图2),点
(如图2),点 在线段
在线段 上,
上, .
.
(1)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)求二面角 的余弦值;
的余弦值; (3)在四棱锥
(3)在四棱锥 的棱
的棱 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若存在,求出
,若存在,求出 点的位置,若不存在,请说明理由.
点的位置,若不存在,请说明理由.
(本小题满分14分)
如图,椭圆
 的离心率为
的离心率为 ,其两焦点分别为
,其两焦点分别为 ,
, 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足 ,过
,过 作倾斜角互补的两条直线
作倾斜角互补的两条直线
 分别交椭圆于
分别交椭圆于
 两点.
两点.
(1)求椭圆
 的方程.
的方程.
(2)求 点坐标;
点坐标; 
(3)当直线 的斜率为
的斜率为 时,求直线
时,求直线 的方程.
的方程. 
.(本小题满分14分)
已知数列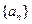 的相邻两项
的相邻两项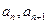 是关于
是关于 的方程
的方程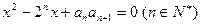 的两实根,且
的两实根,且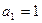 ,记数列
,记数列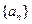 的前
的前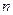 项和为
项和为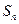 .
.
(1)求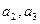 ;
;
(2)求证:数列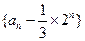 是等比数列;
是等比数列;
(3) 设
设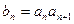 ,问是否存在常数
,问是否存在常数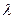 ,使得
,使得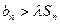 对
对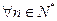 都成立,若存在,
都成立,若存在,
求出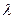 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.