已知集合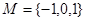 和
和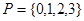 关系的韦恩(venn)图如图所示,则阴影部分所示的集合是( )
关系的韦恩(venn)图如图所示,则阴影部分所示的集合是( )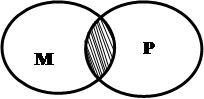
A.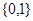 |
B.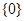 |
C.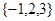 |
D.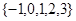 |
设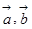 为向量。则
为向量。则 是
是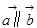 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也必要条件 |
执行右面的框4图,若输出的结果为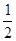 ,则输入的实数
,则输入的实数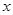 的值是( )
的值是( )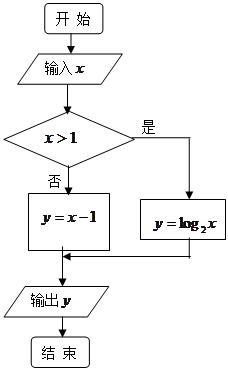
A.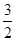 |
B.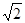 |
C.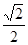 |
D.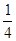 |
甲校有3600名学生,乙校有5400名学生,丙校有学生1800名学生,为统计三校学生的一些方面的情况,计划采用分层抽样的方法抽取一个容量为90人的样本,应在这三校分别抽取学生( )
A.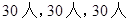 |
B.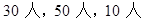 |
C.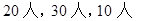 |
D.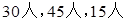 |
已知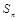 为等差数列
为等差数列 的前
的前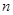 项和,
项和,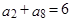 ,则
,则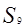 为( )
为( )
A.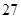 |
B.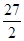 |
C.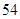 |
D.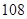 |
函数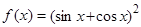 的最小正周期为( )
的最小正周期为( )
A.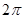 |
B.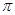 |
C.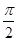 |
D.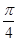 |
关于直线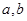 及平面
及平面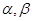 ,下列命题中正确的是( )
,下列命题中正确的是( )
A.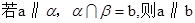 |
B.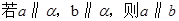 |
C.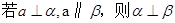 |
D.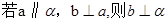 |
已知过点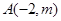 和点
和点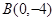 的直线与直线
的直线与直线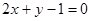 平行,则实数
平行,则实数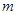 的值为( )
的值为( )
A.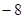 |
B. |
C. | D.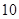 |
对于 上可导的任意函数
上可导的任意函数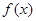 ,若满足
,若满足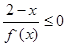 ,则必有( )
,则必有( )
A.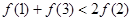 |
B.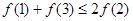 |
C.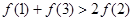 |
D.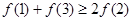 |
定义函数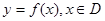 ,若存在常数
,若存在常数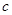 ,对任意
,对任意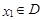 ,存在唯一
,存在唯一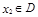 的,使得
的,使得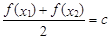 ,则称函数
,则称函数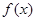 在
在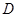 上的均值为
上的均值为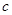 ,已知
,已知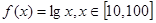 ,则函数
,则函数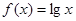 在
在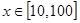 上的均值为。( )
上的均值为。( )
A.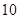 |
B.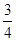 |
C.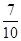 |
D.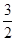 |
函数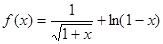 的定义域是_________________________
的定义域是_________________________
如图,某几何体的主视图、左视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积等于____________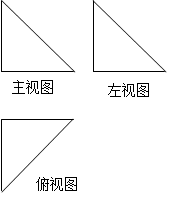
设 满足约束条件
满足约束条件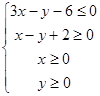 ,则目标函数
,则目标函数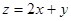 最大值为______
最大值为______
对于实数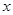 ,用
,用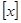 表示不超过
表示不超过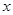 的最大整数,如
的最大整数,如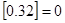 ,
, ,若
,若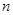 为正整数,
为正整数,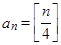 ,
,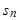 为数列
为数列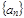 的前
的前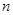 项和,则
项和,则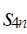 __________________________;
__________________________;
在直角坐标系中,曲线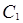 的参数方程为
的参数方程为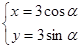 ;在极坐标系(以原点为坐标原点,以轴正半轴为极轴)中曲线
;在极坐标系(以原点为坐标原点,以轴正半轴为极轴)中曲线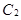 的方程为
的方程为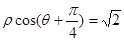 ,则
,则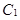 与
与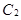 的交点的距离为__________
的交点的距离为__________
如图,割线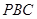 经过圆心
经过圆心 ,
,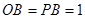 ,
,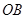 绕点
绕点 逆时针旋
逆时针旋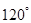 转到
转到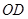 ,连
,连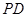 交圆
交圆 于点
于点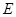 ,则
,则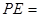 ______________________
______________________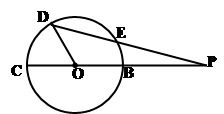
不等式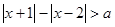 解集为
解集为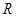 ,则实数
,则实数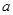 的取值范围为_________________
的取值范围为_________________
各项均为正数的等比数列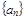 中,
中,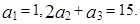
(Ⅰ)求数列 通项公式;
通项公式;
(Ⅱ)若等差数列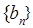 满足
满足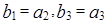 ,求数列
,求数列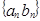 的前
的前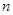 项和
项和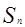 。
。
在△ABC中,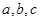 分别为角
分别为角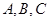 所对的三边,已知
所对的三边,已知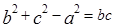
(Ⅰ)求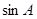 的值
的值
(Ⅱ)若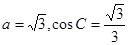 ,求边
,求边 的长.
的长.
()如图,四棱锥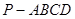 中,
中,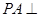 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形,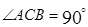 ,
,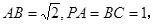
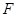 是
是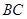 的中点
的中点
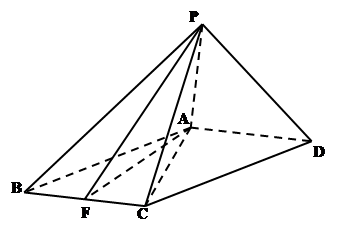
(Ⅰ)求证: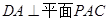
(Ⅱ)试在线段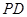 上确定一点
上确定一点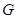 ,使
,使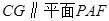 ,求三棱锥
,求三棱锥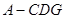 的体积.
的体积.
为了调查学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为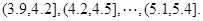 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表
| 分组 |
频数 |
频率 |
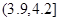 |
3 |
0.06 |
 |
6 |
0.12 |
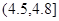 |
25 |
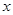 |
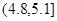 |
 |
 |
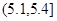 |
2 |
0.04 |
| 合计 |
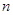 |
1.00 |
(Ⅰ)求频率分布表中未知量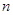 ,
,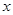 ,
,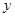 ,
,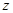 的值
的值
(Ⅱ)从样本中视力在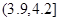 和
和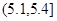 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于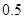 的概率
的概率
在平面直角坐标系 中,已知圆心在
中,已知圆心在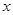 轴上,半径为
轴上,半径为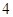 的圆
的圆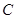 位于
位于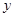 轴的右侧,且与
轴的右侧,且与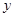 轴相切,
轴相切,
(Ⅰ)求圆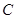 的方程;
的方程;
(Ⅱ)若椭圆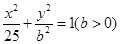 的离心率为
的离心率为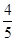 ,且左右焦点为
,且左右焦点为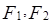 ,试探究在圆
,试探究在圆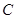 上是否存在点
上是否存在点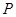 ,使得
,使得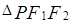 为直角三角形?若存在,请指出共有几个这样的
为直角三角形?若存在,请指出共有几个这样的 点?并说明理由(不必具体求出这些点的坐标)
点?并说明理由(不必具体求出这些点的坐标)
已知函数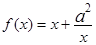 ,
,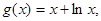 其中
其中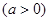
(Ⅰ)若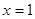 是函数
是函数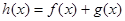 的极值点,求实数
的极值点,求实数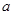 的值;
的值;
(Ⅱ)若对任意的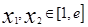 (
(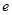 为自然对数的底数)都有
为自然对数的底数)都有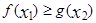 成立,求实数
成立,求实数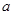 的取值范围
的取值范围