符号“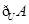 ”可表示为
”可表示为
A.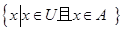 |
B.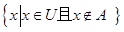 |
C.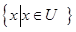 |
D.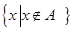 |
 的值等于
的值等于
A. |
B. |
C. |
D. |
下列函数中,既是奇函数又在定义域上是增函数的为
A. |
B. |
C. |
D. |
已知 ,则
,则 的值是
的值是
A. |
B. |
C. |
D. |
三个数 ,
, 之间的大小关系是
之间的大小关系是
A. |
B. |
C. |
D. |
函数 的图象可能是
的图象可能是 
函数 的零点所在的区间是
的零点所在的区间是
A. |
B. |
C. |
D. |
要得到函数 的图象,只需将
的图象,只需将 的图象
的图象
A.向右平移 个单位长度 个单位长度 |
B.向左平移 个单位长度 个单位长度 |
C.向右平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
汽车的油箱是长方体形状容器,它的长是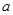 cm,宽是
cm,宽是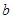 cm,高是
cm,高是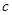 cm,汽车开始行驶时油箱内装满汽油,已知汽车的耗油量是
cm,汽车开始行驶时油箱内装满汽油,已知汽车的耗油量是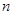 cm3/km,汽车行驶的路程
cm3/km,汽车行驶的路程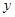 (km)与油箱剩余油量的液面高度
(km)与油箱剩余油量的液面高度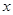 (cm)的函数关系式为
(cm)的函数关系式为
A. |
B.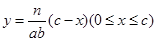 |
C.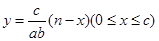 |
D.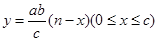 |
设函数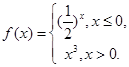 若
若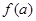 >1,则a的取值范围是
>1,则a的取值范围是
| A.(-1,1) | B.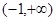 |
C.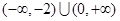 |
D.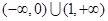 |
已知集合 ,则
,则 ___________.
___________.
若角 的终边经过点
的终边经过点 ,且
,且 ,则
,则 的值为 .
的值为 .
求值: = .
= .
已知 是奇函数,且
是奇函数,且 ,则
,则 .
.
设当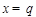 时,函数
时,函数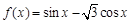 取得最大值,则
取得最大值,则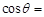 .
.
给定 ,设函数
,设函数 满足:对于任意大于
满足:对于任意大于 的正整数
的正整数 ,
, .
.
(1)设 ,则
,则 ;
;
(2)设 ,且当
,且当 时,
时, ,则不同的函数
,则不同的函数 的个数为 .
的个数为 .
已知:函数 的定义域为
的定义域为 ,集合
,集合 .
.
(Ⅰ)求集合 ;
;
(Ⅱ)求 .
.
已知函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ) 求函数 的单调递增区间.
的单调递增区间.
已知函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)用函数单调性的定义证明函数 在
在 上是减函数.
上是减函数.
已知函数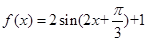 .
.
(Ⅰ)当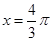 时,求
时,求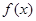 值;
值;
(Ⅱ)若存在区间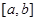 (
(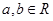 且
且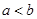 ),使得
),使得 在
在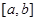 上至少含有6个零
上至少含有6个零
点,在满足上述条件的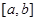 中,求
中,求 的最小值.
的最小值.
已知函数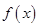 的自变量的取值区间为A,若其值域区间也为A,则称A为
的自变量的取值区间为A,若其值域区间也为A,则称A为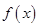 的保值区间.
的保值区间.
(Ⅰ)求函数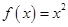 形如
形如 的保值区间;
的保值区间;
(Ⅱ)函数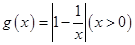 是否存在形如
是否存在形如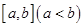 的保值区间?若存在,求出实数
的保值区间?若存在,求出实数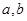 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.