已知全集 ,集合
,集合 ,
, ,那么集合
,那么集合 ( )
( )
A. |
B. |
C. |
D. |
函数
 ( )
( )
A. |
B. |
C. |
D. |
已知点 ,点
,点 ,向量
,向量 ,若
,若 ,则实数
,则实数 的值为( )
的值为( )
| A.5 | B.6 | C.7 | D.8 |
已知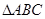 中,
中,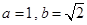 ,
,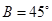 ,则角
,则角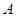 等于( )
等于( )
A.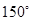 |
B.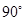 |
C.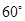 |
D.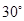 |
设等比数列 的前
的前 项和为
项和为 ,若
,若 ,则下列式子中数值不能确定的是( )
,则下列式子中数值不能确定的是( )
A. |
B. |
C. |
D. |
等比数列{an}中,其公比q<0,且a2=1-a1,a4=4-a3,则a4+a5等于( )
| A.8 | B.-8 | C.16 | D.-16 |
椭圆 的弦被点
的弦被点 平分,则此弦所在的直线方程是( )
平分,则此弦所在的直线方程是( )
A. |
B. |
C. |
D. |
函数f(x)=ln(4+3x-x2)的递减区间是( )
A. |
B. |
C. |
D. |
已知函数 (m为常数)图象上A处的切线与
(m为常数)图象上A处的切线与 平行,则点A的横坐标是( )
平行,则点A的横坐标是( )
A. |
B.1 | C. 或 或 |
D. 或 或 |
已知向量a ,若向量
,若向量 与
与 垂直,则
垂直,则 的值为( )
的值为( )
A. |
B.7 | C. |
D. |
已知命题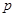 :
: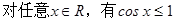 ,则( )
,则( )
A. |
B. |
C. |
D. |
函数f(x)=sin(2x+ )图象的对称轴方程可以为( )
)图象的对称轴方程可以为( )
A.x=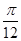 |
B.x= |
C.x= |
D.x= |
如果函数f(x)=ax2+2x-3在区间(-∞,4)上是单调递增的,则实数a的取值范围是__________.
点P(x,y)在直线x+y-4=0上,则x2+y2的最小值是________.
若实数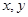 满足条件
满足条件 则
则 的最大值为_____.
的最大值为_____.
双曲线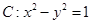 的渐近线方程为_____; 若双曲线
的渐近线方程为_____; 若双曲线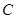 的右顶点为
的右顶点为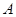 ,过
,过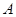 的直线
的直线 与双曲线
与双曲线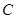 的两条渐近线交于
的两条渐近线交于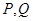 两点,且
两点,且 ,则直线
,则直线 的斜率为_____.
的斜率为_____.
已知函数 .
.
(Ⅰ)若点 在角
在角 的终边上,求
的终边上,求 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求
,求 的值域.
的值域.
已知椭圆 (
( )的右焦点为
)的右焦点为 ,离心率为
,离心率为 .
.
(Ⅰ)若 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线 与椭圆相交于
与椭圆相交于 ,
, 两点,
两点, 分别为线段
分别为线段 的中点. 若坐标原点
的中点. 若坐标原点 在以
在以 为直径的圆上,且
为直径的圆上,且 ,求
,求 的取值范围.
的取值范围.
设函数 在
在 及
及 时取得极值.
时取得极值.
(1)求a、b的值;(2)若对于任意的 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.
已知数列 的前
的前 项和
项和 ,数列
,数列 满足
满足
 .
.
(Ⅰ)求数列 的通项
的通项 ;(Ⅱ)求数列
;(Ⅱ)求数列 的通项
的通项 ;
;
(Ⅲ)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知椭圆 ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 有相同的离心率.
有相同的离心率.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆 和
和 上,
上,  ,求直线
,求直线 的方程.
的方程.
已知函数 .
.
(Ⅰ)若曲线 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.