集合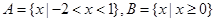 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
圆 的圆心坐标是( )
的圆心坐标是( )
A. |
B. |
C. |
D. |
函数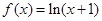 的定义域是( )
的定义域是( )
A. |
B. |
C. |
D. |
已知一个四棱锥的三视图如图所示,则该四棱锥的四个侧面中,直角三角形的个数是( )
| A.4 | B.3 | C.2 | D.1 |
已知点 、
、 ,则线段
,则线段 的垂直平分线的方程是 ( )
的垂直平分线的方程是 ( )
A. |
B. |
C. |
D. |
已知直线 与平面
与平面 ,给出下列三个结论:①若
,给出下列三个结论:①若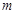 ∥
∥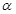 ,
, ∥
∥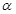 ,则
,则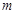 ∥
∥ ;
;
②若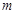 ∥
∥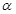 ,
, ,则
,则 ; ③若
; ③若 ,
,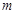 ∥
∥ ,则
,则 .
.
其中正确的个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
设 ,则在下列区间中,使函数
,则在下列区间中,使函数 有零点的区间是( )
有零点的区间是( )
A. |
B. |
C. |
D.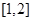 |
如图,长方体 中,
中, ,点
,点 分别是
分别是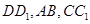 的中点,则异面直线
的中点,则异面直线 与
与 所成的角是 ( )
所成的角是 ( )
| A.30° | B.45° | C.60° | D.90° |
过圆 上的一点
上的一点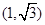 的圆的切线方程是 ( )
的圆的切线方程是 ( )
A. |
B.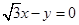 |
C. |
D. |
已知圆 :
: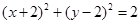 ,圆
,圆 与圆
与圆 关于直线
关于直线 对称,则圆
对称,则圆 的方程为 ( )
的方程为 ( )
A. |
B. |
C.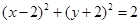 |
D. |
已知 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在 上是增函数,则一定有( )
上是增函数,则一定有( )
A. |
B.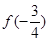 ≥ ≥ |
C. |
D.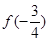 ≤ ≤ |
在直角坐标系 中,设
中,设 ,沿
,沿 轴把坐标平面折成
轴把坐标平面折成 的二面角后,
的二面角后, 的长是 ( )
的长是 ( )
A.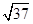 |
B.6 | C. |
D.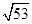 |
已知正方体的棱长为2,则它的内切球的表面积是
已知 ,若
,若 ,则
,则 _______
_______
若直线 被两平行线
被两平行线 所截得的线段的长为
所截得的线段的长为 ,则直线
,则直线 的斜率可以是: ①
的斜率可以是: ① ; ②
; ② ; ③
; ③  ; ④
; ④ ; ⑤
; ⑤
其中正确答案的序号是 .
如图 所在平面,
所在平面, 是
是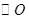 的直径,
的直径, 是
是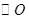 上一点,
上一点, ,
, ,给出下列结论:①
,给出下列结论:①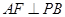 ; ②
; ②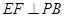 ;③
;③ ; ④平面
; ④平面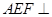 平面
平面 ⑤
⑤ 是直角三角形
是直角三角形
其中正确的命题的序号是 
已知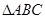 的三个顶点为
的三个顶点为 .
.
(Ⅰ)求边 所在的直线方程; (Ⅱ)求中线
所在的直线方程; (Ⅱ)求中线 所在直线的方程.
所在直线的方程.
如图所示的四棱锥 中,底面
中,底面 为菱形,
为菱形, 平面
平面 ,
, 为
为 的中点,
的中点,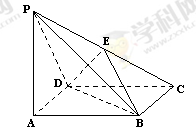
求证:(I)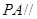 平面
平面 ; (II)平面
; (II)平面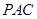 ⊥平面
⊥平面 .
.
设 ,
, ,其中
,其中 且
且 .
.
(I) 若 ,求
,求 的值; (II) 若
的值; (II) 若 ,求
,求 的取值范围.
的取值范围.
如图,在长方体 中,
中,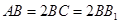 , 沿平面
, 沿平面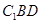 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)
(I)设几何体(1)、几何体(2)的体积分为是 、
、 ,求
,求 与
与 的比值
的比值
(II)在几何体(2)中,求二面角 的正切值
的正切值
已知圆 过点
过点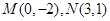 ,且圆心
,且圆心 在直线
在直线 上。
上。
(I)求圆 的方程;
的方程;
(II)问是否存在满足以下两个条件的直线 : ①斜率为
: ①斜率为 ;②直线被圆
;②直线被圆 截得的弦为
截得的弦为 ,以
,以 为直径的圆
为直径的圆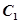 过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由.
过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由.