 是( )
是( )
| A.第一象限角 | B.第二象限角 | C.第三象限角 | D.第四象限角 |
如图,阴影部分表示的集合是( )
A. |
B. |
C. |
D. |
已知角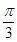 的终边上有一点
的终边上有一点 ,则
,则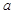 的值是( )
的值是( )
A.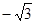 |
B.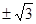 |
C.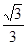 |
D.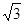 |
已知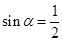 ,则
,则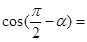 ( )
( )
A.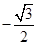 |
B.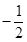 |
C.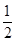 |
D.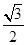 |
若 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. |
B.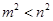 |
C. |
D. |
若函数 为偶函数,且函数
为偶函数,且函数 在
在 上单调递增,则实数
上单调递增,则实数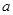 的值为( )
的值为( )
A. |
B.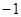 |
C. |
D. |
为了得到函数 的图像,只需将函数
的图像,只需将函数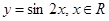 图像上所有的点( )
图像上所有的点( )
A.向左平行移动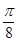 个单位长度 个单位长度 |
B.向右平行移动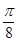 个单位长度 个单位长度 |
C.向左平行移动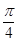 个单位长度 个单位长度 |
D.向右平行移动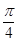 个单位长度 个单位长度 |
已知定义域为 的奇函数
的奇函数 .当
.当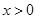 时,
时, ,则不等式
,则不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
若方程 在区间
在区间 内有解,则函数
内有解,则函数 的图像可能是( )
的图像可能是( )
已知 是函数
是函数 的一个零点,若
的一个零点,若 ,则( )
,则( )
A. |
B. |
C. |
D. |
函数 满足
满足 ,且在区间
,且在区间 上的值域是
上的值域是 ,则坐标
,则坐标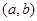 所表示的点在图中的( )
所表示的点在图中的( )
A.线段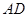 和线段 和线段 上 上 |
B.线段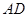 和线段 和线段 上 上 |
C.线段 和线段 和线段 上 上 |
D.线段 和线段 和线段 上 上 |
已知函数 ,若
,若 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
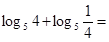 .
.
已知集合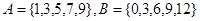 ,则
,则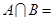 .
.
若 ,且
,且 为第二象限角,则
为第二象限角,则 .
.
已知弧长为
 的弧所对的圆心角为
的弧所对的圆心角为 ,则这条弧所在的扇形面积为
,则这条弧所在的扇形面积为  .
.
已知幂函数 在
在 上单调递减,则实数
上单调递减,则实数 .
.
已知函数 ,
, ,若关于
,若关于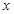 的方程
的方程 有3个不同的实数解,则实数
有3个不同的实数解,则实数 的取值范围是 .
的取值范围是 .
设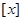 表示不超过
表示不超过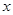 的最大整数,如
的最大整数,如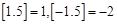 ,若函数
,若函数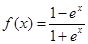 ,则函数
,则函数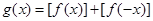 的值域为 .
的值域为 .
已知函数 (其中
(其中 ),满足
),满足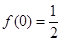 .
.
(Ⅰ)求函数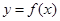 的最小正周期
的最小正周期 及
及 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 的最小值,并且求使函数取得最小值的
的最小值,并且求使函数取得最小值的 的值.
的值.
已知函数 .
.
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)判断函数 的奇偶性;
的奇偶性;
(Ⅲ)若 ,求
,求 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)当 ,函数
,函数 有且仅有一个零点
有且仅有一个零点 ,且
,且 时,求
时,求 的值;
的值;
(Ⅱ)若函数 在区间
在区间 上为单调函数,求
上为单调函数,求 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)若函数 为偶函数,求
为偶函数,求 的值;
的值;
(Ⅱ)若 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,若对任意的
时,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.