已知函数 的定义域为
的定义域为 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设 为虚数单位,若复数
为虚数单位,若复数 是纯虚数,则实数
是纯虚数,则实数 ( )
( )
A. |
B. 或 或 |
C. 或 或 |
D. |
设函数 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 ,则( )
,则( )
A. , , |
B. , , |
C. , , |
D. , , |
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为 的扇形,则该几何体的体积为( )
的扇形,则该几何体的体积为( )
A. |
B. |
C. |
D. |
.给定命题 :若
:若 ,则
,则 ;命题
;命题 :已知非零向量
:已知非零向量 则“
则“ ”是“
”是“ ”的充要条件.则下列各命题中,假命题的是( )
”的充要条件.则下列各命题中,假命题的是( )
A. |
B. |
C. |
D. |
已知函数 .若
.若 ,则
,则 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
执行如图所示的程序框图,若输入 的值为
的值为 ,则输出的
,则输出的 的值为
的值为
A. |
B. |
C. |
D. |
将 个正整数
个正整数 、
、 、
、 、…、
、…、 (
( )任意排成
)任意排成 行
行 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数 、
、 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当 时, 数表的所有可能的“特征值”最大值为
时, 数表的所有可能的“特征值”最大值为
A. |
B. |
C. |
D. |
一个总体分为甲、乙两层,用分层抽样方法从总体中抽取一个容量为 的样本.已知乙层中每个个体被抽到的概率都为
的样本.已知乙层中每个个体被抽到的概率都为 ,则总体中的个体数为 .
,则总体中的个体数为 .
不等式 的解集为_________.
的解集为_________.
若 的值为_______.
的值为_______.
设 是双曲线
是双曲线 的两个焦点,
的两个焦点, 是双曲线与椭圆
是双曲线与椭圆 的一个公共点,则
的一个公共点,则 的面积等于_________.
的面积等于_________.
如果实数 满足
满足 ,若直线
,若直线 将可行域分成面积相等的两部分,则实数
将可行域分成面积相等的两部分,则实数 的值为______.
的值为______.
在极坐标系中,设曲线 与
与 的交点分别为
的交点分别为 、
、 ,则
,则 .
.
如图,从圆 外一点
外一点 引圆的切线
引圆的切线 和割线
和割线 ,已知
,已知 ,
, ,圆
,圆 的半径为
的半径为 ,则圆心
,则圆心 到
到 的距离为 .
的距离为 .
在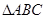 中,角
中,角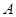 、
、 、
、 的对边分别为
的对边分别为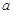 、
、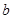 、
、 ,且
,且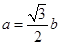 ,
, .
.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 设函数 ,求
,求 的值.
的值.
佛山某中学高三(1)班排球队和篮球队各有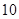 名同学,现测得排球队
名同学,现测得排球队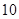 人的身高(单位:
人的身高(单位: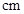 )分别是:
)分别是: 、
、 、
、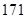 、
、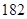 、
、 、
、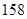 、
、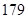 、
、 、
、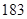 、
、 ,篮球队
,篮球队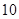 人的身高(单位:
人的身高(单位: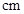 )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、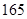 、
、 、
、 、
、 、
、 .
.
(Ⅰ) 请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算);
(Ⅱ) 利用简单随机抽样的方法,分别在两支球队身高超过
 的队员中各抽取一人做代表,设抽取的两人中身高超过
的队员中各抽取一人做代表,设抽取的两人中身高超过
 的人数为
的人数为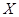 ,求
,求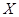 的分布列和数学期望.
的分布列和数学期望.
如图1,矩形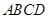 中,
中, ,
, ,
, 、
、 分别为
分别为 、
、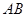 边上的点,且
边上的点,且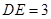 ,
,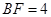 ,将
,将 沿
沿 折起至
折起至 位置(如图2所示),连结
位置(如图2所示),连结 、
、 、
、 ,其中
,其中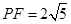 .
.
(Ⅰ)求证: 平面
平面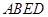 ;
;
(Ⅱ)求直线 与平面
与平面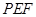 所成角的正弦值.
所成角的正弦值.
如图所示,已知椭圆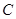 的两个焦点分别为
的两个焦点分别为 、
、 ,且
,且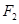 到直线
到直线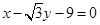 的距离等于椭圆的短轴长.
的距离等于椭圆的短轴长.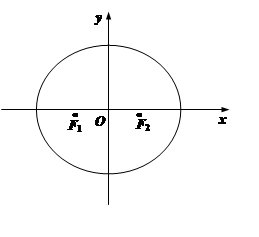
(Ⅰ) 求椭圆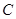 的方程;
的方程;
(Ⅱ) 若圆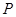 的圆心为
的圆心为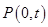 (
(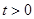 ),且经过
),且经过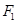 、
、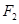 ,
, 是椭圆
是椭圆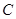 上的动点且在圆
上的动点且在圆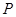 外,过
外,过 作圆
作圆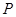 的切线,切点为
的切线,切点为 ,当
,当 的最大值为
的最大值为 时,求
时,求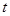 的值.
的值.
数列 、
、 的每一项都是正数,
的每一项都是正数, ,
, ,且
,且 、
、 、
、 成等差数列,
成等差数列, 、
、 、
、 成等比数列,
成等比数列, .
.
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)求数列 、
、 的通项公式;
的通项公式;
(Ⅲ)证明:对一切正整数 ,有
,有 .
.
已知函数 .
.
(Ⅰ)若 ,求
,求 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的极值点;
的极值点;
(Ⅲ)若 恒成立,求
恒成立,求 的取值范围.
的取值范围.