若直线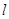 上的一个点在平面α内,另一个点在平面α外,则直线
上的一个点在平面α内,另一个点在平面α外,则直线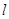 与平面α的位置关系是( )
与平面α的位置关系是( )
A.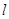  α α |
B.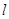  α α |
C.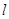 ∥α ∥α |
D.以上都不正确 |
直线x-y+1=0的倾斜角是 ( )
| A.60° | B.45° | C.30° | D.135° |
圆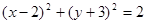 的圆心和半径分别是 ( )
的圆心和半径分别是 ( )
| A.(-2,3), 1 | B. (2,-3), 3 | C. (-2,3), 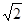 |
D. (2,-3), 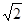 |
在正方体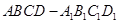 中,异面直线
中,异面直线 与
与 所成的角为 ( )
所成的角为 ( )
A. |
B. |
C.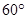 |
D.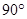 |
过点(1,0)且与直线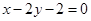 平行的直线方程是 ( )
平行的直线方程是 ( )
A.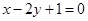 |
B.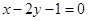 |
C.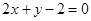 |
D.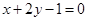 |
点P(1,2,2)是空间直角坐标系中的一点,设它关于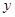 轴的对称点为Q,则PQ的长为( )
轴的对称点为Q,则PQ的长为( )
A.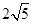 |
B. |
C.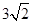 |
D.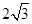 |
下列命题中正确的是 ( )
| A.若一条直线垂直平面内的两条直线,则这条直线与这个平面垂直; |
| B.若一条直线平行平面内的一条直线,则这条直线与这个平面平行; |
| C.若一条直线垂直一个平面,则过这条直线的所有平面都与这个平面垂直; |
| D.若一条直线与两条直线都垂直,则这两条直线互相平行 |
如果直线(2a+5)x+(a-2)y+4=0与直线(2-a)x+(a+3)y-1=0互相垂直,则a的值等于( )
| A.2 | B.-2 | C.2,-2 | D.2,0,-2 |
棱长为2的正方体的顶点都在同一球面上,则该球的表面积为 .
已知直线 //平面
//平面 ,平面
,平面 //平面
//平面 ,则直线
,则直线 与平面
与平面 的位置关系为 .
的位置关系为 .
直线 过
过 ,且
,且 到直线
到直线 距离相等,则直线
距离相等,则直线 的方程
的方程
是 .
若实数 满足
满足 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
①BM与ED平行; ②CN与BE是异面直线;
③CN与BM成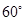 角; ④DM与BN垂直.
角; ④DM与BN垂直.
其中,正确命题的序号是 .
求经过直线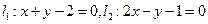 的交点且垂直于直线
的交点且垂直于直线 的直线方程.
的直线方程.
如图所示,一个简单的空间几何体的正视图和侧视图是边长为2 的正三角形,俯视图轮廓为正方形,试描述该几何体的特征,并求该几何体的体积和表面积.
的正三角形,俯视图轮廓为正方形,试描述该几何体的特征,并求该几何体的体积和表面积.
本题满分10分)已知圆C: 与以原点O为圆心的某圆关于直线
与以原点O为圆心的某圆关于直线 对称. (1)求
对称. (1)求 的值;(2)若这时两圆的交点为
的值;(2)若这时两圆的交点为 ,求∠AOB的度数.
,求∠AOB的度数.
如图,四边形ABCD是正方形,PB^平面ABCD,MA^平面ABCD,
PB=AB=2MA. 求证:(1)平面AMD∥平面BPC;(2)平面PMD^平面PBD.
若直线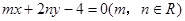 始终平分圆
始终平分圆 的周长,则
的周长,则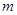 、
、 的关系是 ( )
的关系是 ( )
A. |
B.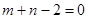 |
C. |
D.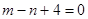 |
已知 、
、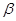 是不同的平面,
是不同的平面, 、
、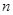 是不同的直线,则下列命题不正确的是 ( )
是不同的直线,则下列命题不正确的是 ( )
A.若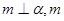 ∥ ∥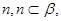 则 则 |
B.若 ∥ ∥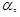  ,则 ,则 ∥ ∥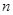 |
C.若 ∥ ∥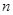 , ,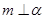 ,则 ,则 |
D.若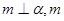  则 则 ∥ ∥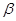 . . |
如图,在四面体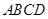 中,截面
中,截面 是正方形,则在下列命题中,错误的为( )
是正方形,则在下列命题中,错误的为( )
A.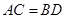 |
B. ∥截面 ∥截面 |
C.异面直线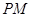 与 与 所成的角为 所成的角为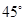 |
D. |

若圆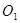 方程为
方程为 ,圆
,圆 方程为
方程为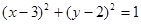 ,则方程
,则方程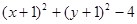
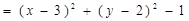 表示的轨迹是 ( )
表示的轨迹是 ( )
A.经过两点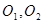 的直线 的直线 |
B.线段 的中垂线 的中垂线 |
| C.两圆公共弦所在的直线 |
| D.一条直线且该直线上的点到两圆的切线长相等 |
如图,已知 与
与 都是边长为
都是边长为 的等边三角形,且平面
的等边三角形,且平面 平面
平面 ,过点
,过点 作
作 平面
平面 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的大小.
所成角的大小.
一只小船以10 m/s的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以20 m/s的速度前进(如图),现在小船在水平面P点以南的40米处,汽车在桥上Q点以西30米处(其中PQ⊥水面),求小船与汽车间的最短距离(不考虑汽车与小船本身的大小).
已知圆C: .
.
(1)若圆C的切线在x轴和y轴上的截距相等,且截距不为零,求此切线的方程;
(2)从圆C外一点P( 、
、 )向该圆引一条切线,切点为M,O为坐标原点,且有
)向该圆引一条切线,切点为M,O为坐标原点,且有 ,求使得
,求使得 取得最小值的点P的坐标.
取得最小值的点P的坐标.