直线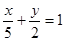 和坐标轴所围成的三角形的面积是
和坐标轴所围成的三角形的面积是
| A.2 | B.5 | C.7 | D.10 |
已知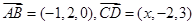 ,若
,若 ,则
,则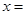
| A.1 | B.4 | C.-1 | D.-4 |
已知 ,则“
,则“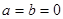 ”是“
”是“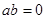 ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面直径与高的比是
A.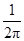 |
B.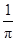 |
C.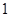 |
D.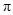 |
已知变量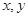 满足约束条件
满足约束条件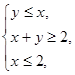 则
则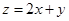 的最大值为
的最大值为
A.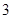 |
B.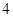 |
C.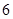 |
D.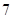 |
若P是平面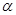 外一点,A为平面
外一点,A为平面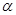 内一点,
内一点,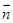 为平面
为平面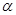 的一个法向量,则点P到平面
的一个法向量,则点P到平面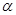 的距离是
的距离是
A.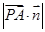 |
B.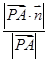 |
C. |
D.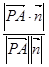 |
.如图,在四面体OABC中,G是底面 ABC的重心,则
ABC的重心,则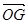 等于
等于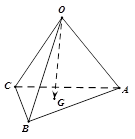
A.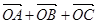 |
B.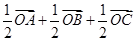 |
C.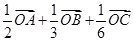 |
D. |
右图是边长相等的两个正方形.给定下列三个命题:
①存在三棱柱,其正视图、侧视图如右图;
②存在四棱柱,其正视图、侧视图如右图;
③存在圆柱,其正视图、侧视图如右图.
其中真命题的个数是
| A.3 | B.2 | C.1 | D.0 |
已知点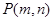 是直线
是直线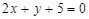 上的任意一点,则
上的任意一点,则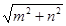 的最小值为
的最小值为
A.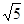 |
B.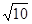 |
C.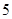 |
D.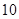 |
设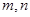 为两条直线,
为两条直线,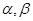 为两个平面,下列四个命题中正确的是
为两个平面,下列四个命题中正确的是
A.若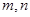 与 与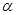 所成的角相等,则 所成的角相等,则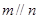 |
B.若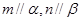 , ,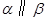 ,则 ,则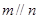 |
C.若 ,则 ,则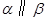 |
D.若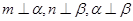 ,则 ,则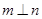 |
如图,正方体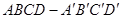 中,
中,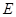 是棱
是棱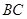 的中点,
的中点,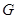 是棱
是棱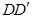 的中点,则异面直线
的中点,则异面直线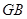 与
与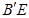 所成的角为
所成的角为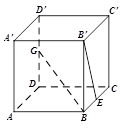
A.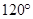 |
B.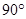 |
C.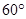 |
D.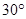 |
已知两点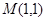 ,
,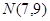 ,点
,点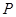 在
在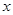 轴或
轴或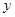 轴上,若
轴上,若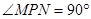 ,则这样的点
,则这样的点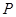 的个数为
的个数为
A.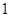 |
B.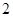 |
C.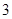 |
D.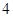 |
已知圆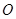 :
: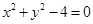 ,圆
,圆 :
: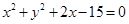 ,若圆
,若圆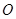 的切线
的切线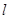 交圆
交圆 于
于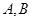 两点,则
两点,则 面积的取值范围是
面积的取值范围是
A.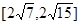 |
B.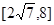 |
C.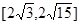 |
D.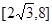 |
命题“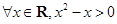 ”的否定是 .
”的否定是 .
两条平行直线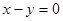 与
与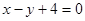 间的距离为 .
间的距离为 .
已知一个几何体的三视图如图所示,则此几何体的体积为 .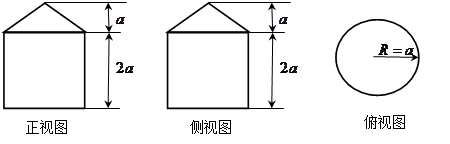
在平面直角坐标系中,不等式组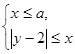 表示的平面区域的面积为
表示的平面区域的面积为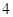 ,则实数
,则实数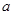 的值是 .
的值是 .
已知三棱锥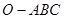 ,侧棱
,侧棱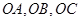 两两互相垂直,且
两两互相垂直,且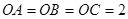 ,则以
,则以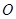 为球心且1为半径的球与三棱锥
为球心且1为半径的球与三棱锥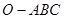 重叠部分的体积是 .
重叠部分的体积是 .
已知点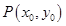 在直线
在直线 上,若圆
上,若圆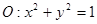 (
(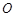 为坐标原点)上存在点
为坐标原点)上存在点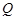 使得
使得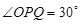 ,则
,则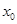 的取值范围为 .
的取值范围为 .
已知函数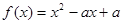 .设
.设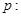 方程
方程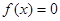 有实数根;
有实数根;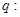 函数
函数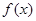 在区间
在区间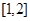 上是增函数.若
上是增函数.若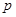 和
和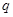 有且只有一个正确,求实数
有且只有一个正确,求实数 的取值范围.
的取值范围.
如图,边长为2的菱形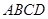 中,
中,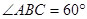 ,点
,点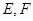 分别是
分别是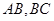 的中点,将
的中点,将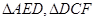 分别沿
分别沿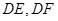 折起,使
折起,使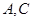 两点重合于点
两点重合于点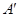 .
.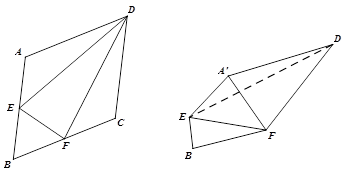 (1)求证:
(1)求证: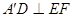 ;
;
(2)求二面角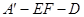 的余弦值.
的余弦值.
已知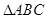 的顶点
的顶点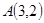 ,
,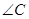 的平分线
的平分线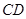 所在直线方程为
所在直线方程为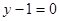 ,
,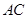 边上的高
边上的高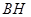 所在直线方程为
所在直线方程为 .
.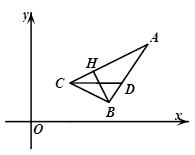
(1)求顶点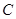 的坐标;
的坐标;
(2)求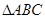 的面积.
的面积.
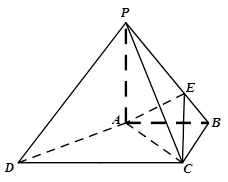
如图,在四棱锥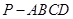 中,
中,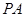 ⊥平面
⊥平面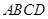 ,底面
,底面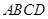 为梯形,
为梯形,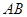 ∥
∥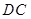 ,
,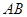 ⊥
⊥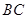 ,
,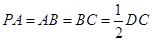 ,点
,点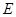 在棱
在棱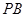 上,且
上,且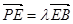 .
.
(1)当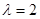 时,求证:
时,求证: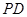 ∥面
∥面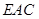 ;
;
(2)若直线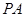 与平面
与平面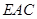 所成角为
所成角为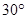 ,求实数
,求实数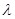 的值.
的值.
已知圆心为点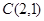 的圆与直线
的圆与直线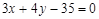 相切.
相切.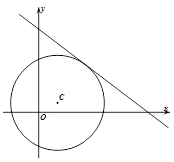
(1)求圆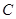 的标准方程;
的标准方程;
(2)对于圆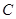 上的任一点
上的任一点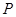 ,是否存在定点
,是否存在定点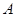 (不同于原点
(不同于原点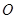 )使得
)使得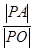 恒为常数?若存在,求出点
恒为常数?若存在,求出点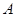 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.