已知角 满足
满足 ,且
,且 ,则角
,则角 的终边在( )
的终边在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
设角 的终边上有一点
的终边上有一点 ,则
,则 的值是( )
的值是( )
A. |
B. |
C. 或 或 |
D.1 |
已知 ,则
,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
如果 ,那么
,那么 ( )
( )
A. |
B. |
C. |
D. |
已知 ,且
,且 与
与 垂直,则
垂直,则 等于( )
等于( )
A. |
B.± |
C.± |
D.± |
已知点 ,若向量
,若向量 与
与 同向,且
同向,且 ,则点
,则点 的坐标为( )
的坐标为( )
A. |
B. |
C. |
D. |
要得到函数 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向右平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向车平移 个单位 个单位 |
设向量 ,若
,若 是实数,且
是实数,且 ,则
,则 的最小值为( )
的最小值为( )
A. |
B.1 | C. |
D. |
求值 .
.
已知向量 ,且
,且 ,则
,则 的值为 .
的值为 .
若 ,则
,则 .
.
已知 是方程
是方程 的两个实数根,则
的两个实数根,则 的值为 .
的值为 .
在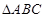 中,
中, ,则
,则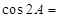 .
.
在 中,设
中,设 ,
, ,且
,且 为直角三角形,求实数
为直角三角形,求实数 的值.
的值.
已知 ,
, 是第三象限角,
是第三象限角, .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
已知函数 的最小正周期为
的最小正周期为 .
.
(1)求函数 的定义域;
的定义域;
(2)求函数 的单调区间.
的单调区间.
已知函数 (
( ,
, 为常数)一段图像如图所示.
为常数)一段图像如图所示.
(1)求函数 的解析式;
的解析式;
(2)将函数 的图像向左平移
的图像向左平移 个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数
个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数 的图像,求函数
的图像,求函数 的单调递增区间.
的单调递增区间.
已知函数 .
.
(1)求函数 的最小正周期和图像的对称轴方程;
的最小正周期和图像的对称轴方程;
(2)求函数 在区间
在区间 上的值域.
上的值域.