已知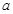 ,
,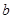 ,
,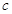 分别是
分别是 的三个内角
的三个内角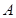 ,
, ,
,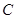 所对的边,若
所对的边,若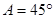 ,
,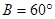 ,
,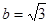 ,则
,则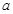 等于
等于
A. |
B.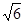 |
C.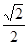 |
D.1 |
在正方体 中,点
中,点 为上底面
为上底面 的中心,若
的中心,若 ,则
,则 ,
, 的值是
的值是
A. , , |
B. , , |
C. , , |
D. , , |
已知两点 ,
, ,且
,且 是
是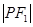 与
与 的等差中项,则动点
的等差中项,则动点 的轨迹方程是
的轨迹方程是
A. |
B.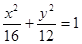 |
C. |
D. |
已知等比数列 的公比为正数,且
的公比为正数,且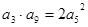 ,
,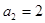 ,则
,则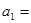
A. |
B. |
C.2 | D. |
双曲线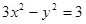 的渐近线方程是
的渐近线方程是
A. |
B.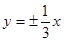 |
C. |
D.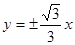 |
设变量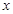 ,
,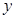 满足约束条件
满足约束条件 ,则
,则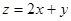 的最大值为
的最大值为
| A.8 | B.6 | C.4 | D. |
下列命题错误的是
A.命题“若 ,则方程 ,则方程 有实数根”的逆否命题是“若方程 有实数根”的逆否命题是“若方程 没有实数根,则 没有实数根,则 ”; ”; |
B.“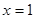 ”是“ ”是“ ”的充分不必要条件; ”的充分不必要条件; |
C.命题“若 ,则 ,则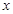 , , 中至少有一个为零”的否命题是“若 中至少有一个为零”的否命题是“若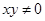 ,则 ,则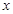 , , 中至多有一个为零”; 中至多有一个为零”; |
D.对于命题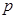 : :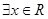 ,使得 ,使得 ;则 ;则 : : ,均有 ,均有 . . |
甲、乙两人同时从图书馆走向教室,甲一半路程步行,一半路程跑步;乙一半时间步行,一半时间跑步,若两人步行、跑步的速度一样,则先到教室的是
| A.甲 | B.乙 | C.甲、乙同时到达 | D.无法确定 |
若关于 的不等式
的不等式 的解集是空集,则实数
的解集是空集,则实数 的取值范围是 .
的取值范围是 .
 中,
中, 在边
在边 上,且
上,且 ,
, ,
, ,
, ,则
,则 的长等于 .
的长等于 .
已知 是等差数列
是等差数列 的前
的前 项和, 且
项和, 且 ,则
,则 .
.
已知双曲线 与椭圆
与椭圆 有共同的焦点,且它们的离心率之和为
有共同的焦点,且它们的离心率之和为 ,则双曲线
,则双曲线 的方程是 .
的方程是 .
过抛物线 的焦点
的焦点 作倾斜角为
作倾斜角为 的直线与抛物线分别交于
的直线与抛物线分别交于 ,
, 两点(
两点( 在
在 轴左侧),则
轴左侧),则 .
.
若正数 ,
, 满足
满足 ,则
,则 的最小值为 .
的最小值为 .
已知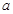 ,
,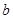 ,
,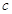 分别是
分别是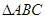 的三个内角
的三个内角 ,
, ,
, 所对的边,且
所对的边,且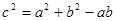 .
.
(1)求角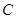 的值;
的值;
(2)若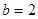 ,
,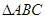 的面积
的面积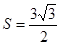 ,求
,求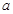 的值.
的值.
已知数列 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 是
是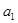 和
和 的等比中项.
的等比中项.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,
, ,试问当
,试问当 为何值时,
为何值时, 最大?并求出
最大?并求出 的最大值.
的最大值.
在直三棱柱 中,
中, ,
, ,异面直线
,异面直线 与
与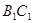 所成的角等于
所成的角等于 ,设
,设 .
.
(1)求 的值;
的值;
(2)求平面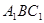 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.
设 ,解关于
,解关于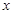 的不等式
的不等式 .
.
设数列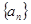 的前
的前 项和为
项和为 ,
, ,
, .证明:数列
.证明:数列 是公比为
是公比为 的等比数列的充要条件是
的等比数列的充要条件是 .
.
在平面直角坐标系中,已知点 ,点
,点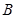 在直线
在直线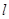 :
: 上运动,过点
上运动,过点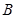 与
与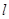 垂直的直线和线段
垂直的直线和线段 的垂直平分线相交于点
的垂直平分线相交于点 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过(1)中的轨迹 上的定点
上的定点
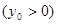 作两条直线分别与轨迹
作两条直线分别与轨迹 相交于
相交于 ,
,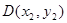 两点.试探究:当直线
两点.试探究:当直线 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,说明理由.