设
 ,
, ,
, ,则
,则
A. |
B. |
C. |
D. |
函数 的定义域为
的定义域为
A. |
B. |
C. |
D. |
直线 平面
平面 ,直线
,直线 平面
平面 ,且
,且 ∥
∥ ,其中
,其中 ,
, 分别是直线
分别是直线 和直线
和直线 在平面
在平面 上的正投影,则直线
上的正投影,则直线 与直线
与直线 的位置关系是
的位置关系是
| A.平行或异面 | B.相交或异面 | C.相交、平行或异面 | D.以上答案都不正确 |
已知空间两点P(-1,2,-3),Q(3,-2,-1),则P、Q两点间的距离是
| A.6 | B.2 | C.36 | D.2 |
.函数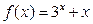 在下列哪个区间内有零点
在下列哪个区间内有零点
A. |
B.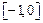 |
C.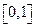 |
D.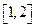 |
若球的半径为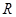 ,则这个球的内接正方体的全面积等于
,则这个球的内接正方体的全面积等于
A.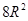 |
B.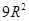 |
C.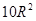 |
D.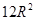 |
函数 得单调递增区间是
得单调递增区间是
A. |
B. |
C. |
D. |
油槽储油20m3,若油从一管道等速流出,则50min流完.关于油槽剩余量
Q(m3)和流出时间t(min)之间的关系可表示为
如图,正方体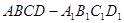 的棱长为1,线段
的棱长为1,线段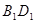 上有两个动点
上有两个动点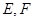 ,且
,且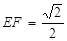 ,则下列结论中错误的是
,则下列结论中错误的是
A.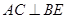 |
B.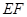 ∥平面 ∥平面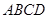 |
C.三棱锥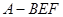 的体积为定值 的体积为定值 |
| D.△AEF与△BEF 的面积相等 |
已知A(2,4)与B(3,3)关于直线l对称,则直线l的方程为
| A.x+y=0 | B.x-y=0 | C.x+y-6=0 | D.x-y+1=0 |
方程x2+y2+2kx+4y+3k+8=0表示圆,则k的取值范围是
| A.k=4或k=-1 | B.k>4或k<-1 | C.-1<k<4 | D.以上都不对 |
圆 的圆心在直线
的圆心在直线 上,经过点
上,经过点 ,且与直线
,且与直线  相切,
相切,
则圆 的方程为
的方程为
A. |
B. |
C. |
D. |
已知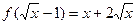 ,则
,则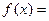 ××××××.
××××××.
一个正三棱锥的底面边长为6,侧棱长为,那么这个正三棱锥的体积是
××××× ×.
×.
若直线 过点
过点 斜率为1,圆
斜率为1,圆 上恰有3个点到
上恰有3个点到 的距离为1,
的距离为1,
则 的值为××××××.
的值为××××××.
.若 满足2x+
满足2x+ ="5,"
="5,"  满足2x+2
满足2x+2 (x
(x 1)="5," 则
1)="5," 则 +
+ = ××××××.
= ××××××.
(本小题满分10分)
如图所示的一个三视图中,右面是一个长方体截去一角所得多面体的直观图,它的正视 图和侧视图在下面画出(单位:cm)
图和侧视图在下面画出(单位:cm)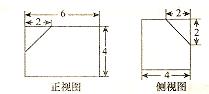
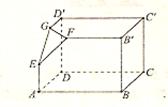
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(本小题满分12分)
已知两直线 :
: 和
和 :
: ,
,
(1)若 与
与 交于点
交于点 ,求
,求 的值;
的值;
(2)若 ,试确定
,试确定 需要满足的条件;
需要满足的条件;
(3)若l1⊥l2 ,试确定 需要满足的条件.
需要满足的条件.
(本小题满分12分)
已知函数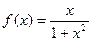 .
.
(1)判断其奇偶性;
(2)指出该函数在区间(0,1)上的单调性并证明;
(3)利用(1)、(2)的结论,指出该函数在(-1,0)上的增减性.
.(本题满分12分)
如图所示,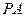 ⊥矩形
⊥矩形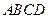 所在的平面,
所在的平面,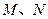 分别是
分别是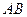 、
、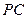 的中点,
的中点,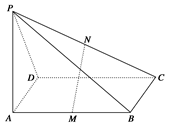
(1)求证: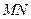 ∥平面
∥平面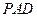 ;
;
(2)求证: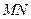 ⊥
⊥ ;
;
(3)若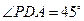 ,求证:平面
,求证:平面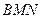 ⊥平面
⊥平面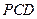 .
.
(本小题满分12分)
已知函数 且
且 在区间[,4]上的最大值与最小值的差为3,求
在区间[,4]上的最大值与最小值的差为3,求 .
.
.(本小题满分12分)
已知点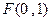 ,一动圆过点
,一动圆过点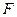 且与圆
且与圆 内切,
内切,
(1)求动圆圆心的轨迹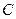 的方程;
的方程;
(2)设点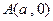 ,点
,点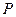 为曲线
为曲线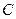 上任一点,求点
上任一点,求点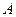 到点
到点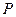 距离的最大值
距离的最大值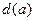 ;
;
(3)在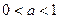 的条件下,设△
的条件下,设△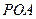 的面积为
的面积为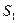 (
(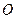 是坐标原点,
是坐标原点,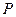 是曲线
是曲线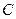 上横坐标为
上横坐标为 的点),以
的点),以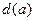 为边长的正方形的面积为
为边长的正方形的面积为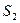 .若正数
.若正数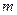 满足
满足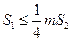 ,问
,问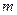 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.