已知全集 ,若集合
,若集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
过点 且倾斜角为
且倾斜角为 的直线方程为( )
的直线方程为( )
A. |
B. |
C. |
D. |
某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润 与时间
与时间 的关系,可选用( )
的关系,可选用( )
| A.一次函数 | B.二次函数 | C.指数型函数 | D.对数型函数 |
点 和点
和点 关于直线
关于直线 对称,则( )
对称,则( )
A. |
B. |
C. |
D. |
已知某几何体的三视图如图,则该几何体的体积是( )
A. |
B. |
C. |
D. |
已知直线上两点 的坐标分别为
的坐标分别为 ,且直线与直线
,且直线与直线 垂直,则
垂直,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
函数 的图像大致是( )
的图像大致是( )
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. |
B. |
C. |
D. |
下列函数中既是奇函数又是 上的增函数的是( )
上的增函数的是( )
A. |
B. |
C. |
D. |
已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为 ,则该三棱锥的外接球的表面积是( )
,则该三棱锥的外接球的表面积是( )
A. |
B. |
C. |
D. |
已知函数 ,
, ,则下列选项正确的是( )
,则下列选项正确的是( )
A. |
B. |
C. |
D. |
已知函数 ,若关于
,若关于 的方程
的方程 有两个不同的根,则实数
有两个不同的根,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
函数 在
在 上的最大值比最小值大
上的最大值比最小值大 ,则
,则 .
.
正方体 中,异面直线
中,异面直线 与
与 所成角度为 .
所成角度为 .
已知两条直线 ,
, 之间的距离为
之间的距离为 ,则
,则 .
.
设、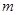 、
、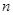 表示不同的直线,
表示不同的直线,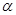 ,
,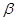 ,
, 表示不同的平面,则下列四个命题正确的是 .
表示不同的平面,则下列四个命题正确的是 .
①若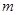 ∥
∥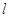 ,且
,且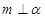 ,则
,则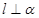 ;②若
;②若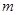 ∥
∥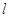 ,且
,且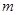 ∥
∥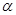 ,则
,则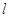 ∥
∥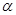 ;③若
;③若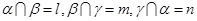 ,则
,则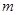 ∥
∥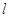 ∥
∥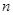 ;④若
;④若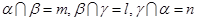 ,且
,且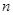 ∥
∥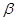 ,则
,则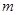 ∥
∥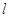 .
.
已知函数 且
且 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性并予以证明.
的奇偶性并予以证明.
如图,已知在四棱锥 中, 底面四边形
中, 底面四边形 是直角梯形,
是直角梯形,  ,
, ,
, .
.
(1)求证: ;
;
(2)求直线 与底面
与底面 所成角的正切值.
所成角的正切值.
已知直线 过点
过点 ,直线
,直线 的斜率为
的斜率为 且过点
且过点 .
.
(1)求 、
、 的交点
的交点 的坐标;
的坐标;
(2)已知点 ,若直线
,若直线 过点
过点 且与线段
且与线段 相交,求直线
相交,求直线 的斜率
的斜率 的取值范围.
的取值范围.
已知在棱长为2的正方体 中,
中, 为
为 的中点.
的中点.
(1)求证: ∥
∥ ;
;
(2)求三棱锥 的体积.
的体积.
某家具厂生产一种儿童用组合床柜的固定成本为20000元,每生产一组该组合床柜需要增加投入100元,已知总收益满足函数: ,其中
,其中 是组合床柜的月产量.
是组合床柜的月产量.
(1)将利润 元表示为月产量
元表示为月产量 组的函数;
组的函数;
(2)当月产量为何值时,该厂所获得利润最大?最大利润是多少?(总收益=总成本+利润).
已知函数 (
( ).
).
(1)证明:当 时,
时, 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时 的单调区间;
的单调区间;
(2)已知函数 ,函数
,函数 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.