设集合
，则
A． |
B． |
C． |
D． |
的值是
A． |
B． |
C． |
D． |
函数
是
A．周期为 的奇函数 |
B．周期为的偶函数 |
C．周期为 的奇函数 |
D．周期为的偶函数 |
下列函数在区间
是增函数的是
A． |
B． |
C． |
D． |
设函数
则
的值为
A． |
B． |
C． |
D． |
已知函数
且
在区间
上的最大值和最小值之和为
，则的值为
A． |
B． |
C． |
D． |
定义一种运算
，则函数
的值域为
A． |
B． |
C． |
D． |
已知
分别是
的边
上的中线，且
，则
A． |
B． |
C． |
D． |
将函数
的图像向左平移
个单位，所得图像关于
轴对称，则
的最小值为
A． |
B． |
C． |
D． |
已知函数
，其中
为实数，若
对
恒成立，且
，则
的单调递增区间是
A． |
B． |
C． |
D． |
函数
的定义域是 ．
计算：
．
已知向量
满足
，且它们的夹角为
，则
．
已知
，则
．
函数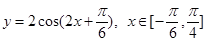
的值域为 ．
设
是定义在
上的奇函数，当
时，
为常数），则
．
若函数
对于
上的任意
都有
，则实数
的取值范围是 ．
已知
．求
和
的值．
（函数
．
（1）若
是偶函数，求实数
的值；
（2）当
时，求
在区间
上的值域．
已知点
是函数
，
）一个周期内图象上的两点，函数
的图象与
轴交于点
，满足
．
（1）求的表达式；
（2）求函数
在区间
内的零点．
已知向量
（
为实数）．
（1）
时，若
，求
；
（2）若
，求
的最小值，并求出此时向量
在
方向上的投影．
已知函数
．
（1）判断函数
在
的单调性并用定义证明；
（2）令
，求
在区间的最大值的表达式
．