和
的等比中项是 .
向量
，若
⊥
，则实数
.
已知
，则
.
向量
，则与
同向的单位向量是 .
三阶行列式
中，元素
的代数余子式的值是 .
数列
中，若
，
，则
.
根据右图所示的程序框图，输出结果
.
数列
中，
则
.
非零向量
，则“
”是“
∥
”的 条件．
2013年12月初，上海遭遇最严重的雾霾天气，空气质量持续重度污染．某教室安装新型空气净化器，每小时可将
含量降低
．该净化器连续工作 小时，可将从
降到
以下．（结果保留整数）
对任意的实数
，矩阵运算
都成立，则
.
若数列
满足
，设
，
，类比课本中推导等比数列前
项和公式的方法，可求得
.
等边
中，向量
的夹角为（ ）
A． |
B． |
C． |
D． |
已知等比数列
，它的前
项为
，前
项和为
，则使得
的的值是（ ）
A． |
B． |
C． |
D． |
用数学归纳法证明“
，
”时，从“
”到“
”左边需要添加的代数式为（ ）
A． |
B． |
C． |
D． |
下列命题正确的是（ ）
A． |
B．若 ，则 |
C．若 ，则 或 |
D．若 ，则 或 |
已知向量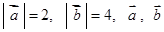
的夹角为
．
（1）求
的值；
（2）求
的大小．
用行列式解关于
的方程组：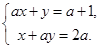
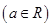，并对解的情况进行讨论．
已知直角坐标平面中，
为坐标原点，
．
（1）求
的大小（结果用反三角函数值表示）；
（2）设点
为
轴上一点，求
的最大值及取得最大值时点的坐标．
已知数列
的前
项和为
，
．
（1）求证：数列是等比数列；
（2）若
，求实数
的取值范围.
平面直角坐标系中，
为原点，射线
与
轴正半轴重合，射线
是第一象限角平分线．在上有点列
，
，在上有点列
，
，．已知
，
，
．
（1）求点
的坐标；
（2）求
的坐标；
（3）求
面积的最大值，并说明理由．