已知集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
某几何体的三视图如图所示,则它的体积是( )
A. |
B. |
C. |
D. |
设 ,则( )
,则( )
A. |
B. |
C. |
D. |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等,则这两条直线平行 |
| B.若一个平面内有不共线的三点到另一个平面的距离相等,则这两个平面平行 |
| C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| D.若两个平面都垂直于第三个平面,则这两个平面平行 |
已知 两点,过动点
两点,过动点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若 ,当
,当 时,动点
时,动点 的轨迹为( )
的轨迹为( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
将正方形 沿对角线
沿对角线 折成一个直二面角,点
折成一个直二面角,点 到达点
到达点 ,则异面直线
,则异面直线 与
与 所成角是( )
所成角是( )
A. |
B. |
C. |
D. |
函数 的图象大致是( )
的图象大致是( )
已知点 ,则与向量
,则与向量 同方向的单位向量是( )
同方向的单位向量是( )
A. |
B. |
C. |
D. |
直线 将圆
将圆 分割成的两段圆孤长之比为( )
分割成的两段圆孤长之比为( )
A. |
B. |
C. |
D. |
已知向量 若
若 则
则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
双曲线 的渐近线与抛物线
的渐近线与抛物线 相切,则该双曲线的离心率等于( )
相切,则该双曲线的离心率等于( )
A. |
B. |
C. |
D. |
已知定义在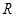 上的可导函数
上的可导函数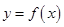 的导函数为
的导函数为 ,满足
,满足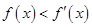 ,且
,且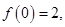 则不等式
则不等式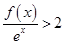 的解集为( )
的解集为( )
A. |
B. |
C. |
D.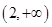 |
双曲线 的顶点到其渐近线的距离等于____________.
的顶点到其渐近线的距离等于____________.
若点 在曲线
在曲线 上移动,设点
上移动,设点 处的切线的倾斜角为
处的切线的倾斜角为 ,则
,则 的范围是______.
的范围是______.
已知直线 交抛物线
交抛物线 于
于 两点.若该抛物线上存在点
两点.若该抛物线上存在点 ,使得
,使得 ,则
,则 的取值范围为_________.
的取值范围为_________.
已知直线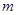 ,
, 和平面
和平面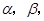 且
且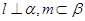 ,给出下列四个命题:
,给出下列四个命题:
① ②
②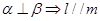 ③
③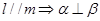 ④
④
其中真命题的有________(请填写全部正确命题的序号)
已知向量 向量
向量 记
记
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 ,求函数
,求函数 的值域.
的值域.
从某年级学生中,随机抽取50人,其体重(单位:千克)的频数分布表如下:
| 分组(体重) |
 |
 |
 |
 |
| 频数(人) |
 |
 |
 |
 |
(1)根据频数分布表计算体重在 的频率;
的频率;
(2)用分层抽样的方法从这50人中抽取10人,其中体重在 中共有几人?
中共有几人?
(3)在(2)中抽出的体重在 的人中,任取2人,求体重在
的人中,任取2人,求体重在 中各有1人的概率.
中各有1人的概率.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面 底面
底面 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形, ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.
(1)求证:EF//平面PAD;
(2)求证:平面 平面
平面 .
.
数列 的前
的前 项和为
项和为 ,且
,且 是
是 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足
(1)求数列 、
、 的通项公式
的通项公式
(2)设 =
= ,求数列
,求数列 的前
的前 项和
项和 .
.
已知函数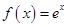 .
.
(1)求函数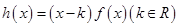 .的单调区间;
.的单调区间;
(2)设函数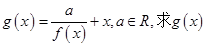 的极值.
的极值.
已知椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,圆
,圆 的直径为
的直径为 的长轴.如图,
的长轴.如图, 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线 过点
过点 且与圆
且与圆 交于
交于 两点,
两点, 垂直于
垂直于 交椭圆于点
交椭圆于点 .
.
(1)求椭圆 的方程;
的方程;
(2)求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.