若 ,则
,则 是
是 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知抛物线 上一点P到y轴的距离为6,则点P到焦点的距离为( )
上一点P到y轴的距离为6,则点P到焦点的距离为( )
| A.7 | B.8 | C.9 | D.10 |
空间四边形ABCD的各顶点坐标分别是 ,E,F分别是AB与CD的中点,则EF的长为( )
,E,F分别是AB与CD的中点,则EF的长为( )
A. |
B. |
C. |
D.3 |
设数列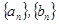 都是等差数列,若
都是等差数列,若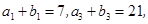 则
则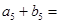 ( )
( )
| A.35 | B.38 | C.40 | D.42 |
不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D.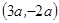 |
双曲线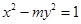 的一个焦点坐标为
的一个焦点坐标为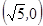 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.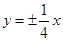 |
B.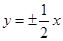 |
C.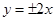 |
D.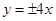 |
设变量 满足
满足 则目标函数
则目标函数 的最小值为( )
的最小值为( )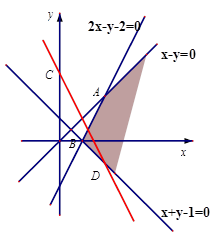
| A.2 | B.4 | C.6 | D.以上均不对 |
在 中,
中,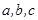 是角A,B,C的对边,若
是角A,B,C的对边,若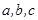 成等比数列,
成等比数列, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设等差数列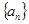 的公差
的公差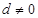 ,
,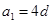 ,若
,若 是
是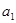 与
与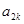 的等比中项,则
的等比中项,则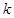 =( )
=( )
| A.3或6 | B.3 | C.3或9 | D.6 |
在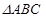 中,角
中,角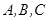 所对的边分别为
所对的边分别为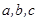 ,若
,若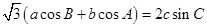 ,
,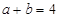 ,且
,且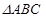 的面积的最大值为
的面积的最大值为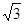 ,则此时
,则此时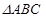 的形状为 ( )
的形状为 ( )
| A.锐角三角形 | B.直角三角形 | C.等腰三角形 | D.正三角形 |
已知等差数列 的通项公式为
的通项公式为 ,设
,设 ,则当
,则当 取得最小值是,n的值是 ( )
取得最小值是,n的值是 ( )
| A.17 | B.16 | C.15 | D.13 |
抛物线 的焦点F恰好是双曲线
的焦点F恰好是双曲线 的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 ( )
的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 ( )
A. |
B. |
C.3 | D. |
已知数列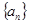 为等比数列,
为等比数列,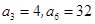 ,则
,则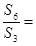 .
.
在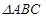 中,
中,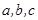 分别是角A,B,C的对边,且
分别是角A,B,C的对边,且 ,则
,则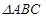 的面积为 .
的面积为 .
已知命题:① 为两个命题,则“
为两个命题,则“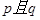 为真”是“
为真”是“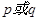 为真”的必要不充分条件;②若
为真”的必要不充分条件;②若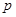 为:
为: ,则
,则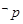 为:
为: ;③命题
;③命题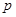 为真命题,命题
为真命题,命题 为假命题,则命题
为假命题,则命题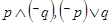 都是真命题;④命题“若
都是真命题;④命题“若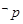 ,则
,则 ”的逆否命题是“若
”的逆否命题是“若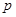 ,则
,则 ”.期中正确命题的序号是 .
”.期中正确命题的序号是 .
如图,椭圆 的离心率
的离心率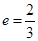 ,左焦点为F,
,左焦点为F,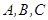 为其三个顶点,直线CF与AB交于点D,则
为其三个顶点,直线CF与AB交于点D,则 的值等于 .
的值等于 .
已知命题 :“不等式
:“不等式 对任意
对任意 恒成立”,命题
恒成立”,命题 :“方程
:“方程 表示焦点在x轴上的椭圆”,若
表示焦点在x轴上的椭圆”,若 为真命题,
为真命题, 为真,求实数
为真,求实数 的取值范围.
的取值范围.
在 中,
中, 分别是角A,B,C的对边,且满足
分别是角A,B,C的对边,且满足 .
.
(1)求角B的大小;
(2)若 最大边的边长为
最大边的边长为 ,且
,且 ,求最小边长.
,求最小边长.
某公司欲建连成片的网球场数座,用288万元购买土地20000平方米,每座球场的建筑面积为1000平方米,球场每平方米的平均建筑费用与所建的球场数有关,当该球场建n座时,每平方米的平均建筑费用 表示,且
表示,且 (其中
(其中 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.
(1)为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几座网球场?
(2)若球场每平方米的综合费用不超过820元,最多建几座网球场?
如图,已知三棱锥 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, , M、N分别是
, M、N分别是 的中点,点P在线段
的中点,点P在线段 上,且
上,且 ,
,
(1)证明:无论 取何值,总有
取何值,总有 .
.
(2)当 时,求平面
时,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
已知数列 前n项和
前n项和 =
= (
( ), 数列
), 数列 为等比数列,首项
为等比数列,首项 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足 ,
, ,
, 为等比数列.
为等比数列.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)设 ,记数列
,记数列 的前n项和为Tn,,求Tn。
的前n项和为Tn,,求Tn。
已知椭圆 的离心率为
的离心率为 ,椭圆的的一个顶点和两个焦点构成的三角形的面积为4,
,椭圆的的一个顶点和两个焦点构成的三角形的面积为4,
(1)求椭圆C的方程;
(2)已知直线 与椭圆C交于A, B两点,若点M(
与椭圆C交于A, B两点,若点M( , 0),求证
, 0),求证 为定值.
为定值.