命题“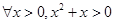 ”的否定是 .
”的否定是 .
右图给出的是一个算法的伪代码,若输入值为 ,则输出值
,则输出值 = .
= . 
函数 的导数
的导数 .
.
先后抛掷一枚质地均匀的骰子(各面上分别标有点数 )两次,骰子朝上的面的点数依次记为
)两次,骰子朝上的面的点数依次记为 和
和 ,则双曲线
,则双曲线 为等轴双曲线的概率为 .
为等轴双曲线的概率为 .
右边程序输出的结果是 .
恒大足球队主力阵容、替补阵容各有 名编号为
名编号为 的球员进行足球点球练习,每人点球
的球员进行足球点球练习,每人点球 次,射中的次数如下表:
次,射中的次数如下表:
| 队员\编号 |
1号 |
2号 |
3号 |
4号 |
| 主力 |
4 |
5 |
3 |
4 |
| 替补 |
5 |
4 |
2 |
5 |
则以上两组数据的方差中较小的方差 .
.
下列有关命题的说法中,错误的是 (填所有错误答案的序号).
①命题“若 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”;
②“ ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件;
③若 为假命题,则
为假命题,则 、
、 均为假命题.
均为假命题.
已知抛物线 的焦点是双曲线
的焦点是双曲线 的右焦点,则双曲线的渐近线方程为 .
的右焦点,则双曲线的渐近线方程为 .
底面边长为 ,高为
,高为 的正三棱锥的全面积为
的正三棱锥的全面积为  .
.
奇函数 在
在 处有极值,则
处有极值,则 的值为 .
的值为 .
若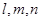 是三条互不相同的空间直线,
是三条互不相同的空间直线, 是两个不重合的平面,
是两个不重合的平面,
则下列命题中为真命题的是 (填所有正确答案的序号).
①若 则
则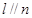 ; ②若
; ②若 则
则 ;
;
③若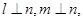 则
则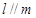 ; ④若
; ④若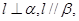 则
则
设集合 ,且
,且 ,在直角坐标平面内,从所有满足这些条件的有序实数对
,在直角坐标平面内,从所有满足这些条件的有序实数对 所表示的点中任取一个,若该点落在圆
所表示的点中任取一个,若该点落在圆 内的概率为
内的概率为 ,则满足要求的
,则满足要求的 的最小值为 .
的最小值为 .
如图平面直角坐标系 中,椭圆
中,椭圆 的离心率
的离心率 ,
, 分别是椭圆的左、右两个顶点,圆
分别是椭圆的左、右两个顶点,圆 的半径为
的半径为 ,过点
,过点 作圆
作圆 的切线,切点为
的切线,切点为 ,在
,在 轴的上方交椭圆于点
轴的上方交椭圆于点 .则
.则 .
.
设奇函数 定义在
定义在 上,其导函数为
上,其导函数为 ,且
,且 ,当
,当 时,
时, ,则关于
,则关于 的不等式
的不等式 的解集为 .
的解集为 .
根据我国发布的《环境空气质量指数 技术规定》(试行),
技术规定》(试行), 共分为六级:
共分为六级: 为优,
为优, 为良,
为良, 为轻度污染,
为轻度污染, 为中度污染,
为中度污染, 均为重度污染,
均为重度污染, 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份 天的
天的 的频率分布直方图如图所示:
的频率分布直方图如图所示:
⑴该市11月份环境空气质量优或良的共有多少天?
⑵若采用分层抽样方法从 天中抽取
天中抽取 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
⑶空气质量指数低于 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
已知命题 表示双曲线,命题
表示双曲线,命题 表示椭圆.
表示椭圆.
⑴若命题 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
⑵判断命题 为真命题是命题
为真命题是命题 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
如图,直三棱柱 中,点
中,点 是
是 上一点.
上一点.
⑴若点 是
是 的中点,求证
的中点,求证 平面
平面 ;
;
⑵若平面 平面
平面 ,求证
,求证 .
.
如图,储油灌的表面积 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
⑴试用半径 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 的范围.
的范围.
⑵当圆柱高 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积 最大?
最大?
如图,椭圆 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆 的长轴长为
的长轴长为 ,且椭圆
,且椭圆 的左准线
的左准线 被椭圆
被椭圆 截得的线段
截得的线段 长为
长为 ,已知点
,已知点 是椭圆
是椭圆 上的一个动点.
上的一个动点.
⑴求椭圆 与椭圆
与椭圆 的方程;
的方程;
⑵设点 为椭圆
为椭圆 的左顶点,点
的左顶点,点 为椭圆
为椭圆 的下顶点,若直线
的下顶点,若直线 刚好平分
刚好平分 ,求点
,求点 的坐标;
的坐标;
⑶若点 在椭圆
在椭圆 上,点
上,点 满足
满足 ,则直线
,则直线 与直线
与直线 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
已知函数 .
.
⑴当 时,①若
时,①若 的图象与
的图象与 的图象相切于点
的图象相切于点 ,求
,求 及
及 的值;
的值;
② 在
在 上有解,求
上有解,求 的范围;
的范围;
⑵当 时,若
时,若 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.