集合 ,则实数m的取值范围( )
,则实数m的取值范围( )
A. |
B. |
C. |
D. |
过点 的直线
的直线 将圆
将圆 分成两段弧,当其中的劣弧最短时,直线
分成两段弧,当其中的劣弧最短时,直线 的方程是
的方程是
A. |
B. |
C. |
D. |
已知 =(cos
=(cos π, sin
π, sin π),
π),  ,
,  ,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )
,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )
| A.1 | B. |
C.2 | D. |
.已知二次函数 ,当n依次取
,当n依次取 时,其图像在
时,其图像在 轴上所截得的线段的长度的总和为( )
轴上所截得的线段的长度的总和为( )
| A.1 | B. |
C. |
D. |
.若 为奇函数, 且在[0,
为奇函数, 且在[0, ]为增函数, 则
]为增函数, 则 的一个值为
的一个值为
A. |
B.- |
C. |
D.- |
在圆 内,过点
内,过点 有n条弦的长度成等差数列,最短弦长为数列的首项
有n条弦的长度成等差数列,最短弦长为数列的首项 ,最长弦长为
,最长弦长为 ,若公差
,若公差 ,那么n的取值集合为 ( )
,那么n的取值集合为 ( )
A. |
B. |
C. |
D. |
.如果函数 (a为常数)在区间
(a为常数)在区间 内单调递增,
内单调递增,
且在区间(0,2)内单调递减,则常数a的值为( )
| A. 1 | B. 2 | C.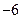 |
D. |
设 、
、 、
、 、
、 是半径为
是半径为 的球面上的四点,且满足
的球面上的四点,且满足 ,
, ,
, ,则
,则 的最大值是 ( )
的最大值是 ( )
A. |
B. |
C. |
D. |
.已知 ,满足
,满足 有
有 恒成立,且
恒成立,且
 与
与 的大小为 ( )
的大小为 ( )
A. |
B. |
C. |
D. 大小不定 大小不定 |
已知 的导函数是
的导函数是 ,记
,记
 则 ( )
则 ( )
| A.A>B>C | B.A>C>B | C.B>A>C | D.C>B>A |
若 、
、 两点分别在圆
两点分别在圆 上运动,
上运动,
则 的最大值为( )
的最大值为( )
| A.13 | B.19 | C.32 | D.38. |
已知 是
是 上的奇函数,
上的奇函数,
 ,则数列
,则数列 的通项公式为 ( )
的通项公式为 ( )
A. |
B. |
C. |
D. |

已知关于 的方程
的方程 的两根为
的两根为 和
和 ,
, ,
,
则 的值为 。
的值为 。
若直线 始终平分圆
始终平分圆 的周长,则
的周长,则 的最小值为 。
的最小值为 。
向量 ,
, 为坐标原点,动点
为坐标原点,动点 满足
满足 ,
,
则点 构成图形的面积为 .
构成图形的面积为 .
(本小题满分10分) 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为 、
、 、
、 ,
,
已知
(1)求 的值; (2)求
的值; (2)求 的面积。
的面积。
.(本小题满分12分)已知函数 .若
.若 为整数,且函数
为整数,且函数 在
在 内恰有一个零点,求
内恰有一个零点,求 的值.
的值.
..(本小题满分12分)如图,在正方体 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)如果 ,一个动点从点
,一个动点从点 出发在正方体的
出发在正方体的
表面上依次经过棱 、
、 、
、 、
、 、
、 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
.(本小题满分12分)数列 的前
的前 项和记为
项和记为 ,
,
(1) 求 的通项公式;
的通项公式;
(2) 等差数列 的各项为正,其前
的各项为正,其前 项和为
项和为 ,且
,且 ,
,
.本小题满分12分)已知函数
 是R上的奇函数,
是R上的奇函数,
当 时
时 取得极值
取得极值 ,
,
(1)求 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意 ,不等式
,不等式 恒成立. 、
恒成立. 、
.已知 ,函数
,函数 .
.
(1)若函数 在区间
在区间 内是减函数,求实数
内是减函数,求实数 的取值范围;
的取值范围;
(2)求函数 在区间
在区间 上的最小值
上的最小值 ;
;
(3)对(2)中的 ,若关于
,若关于 的方程
的方程 有两个不相等的实数解,
有两个不相等的实数解,
求实数 的取值范围.
的取值范围.