命题“若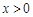 ,则
,则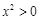 ”的否命题为 .
”的否命题为 .
若直线 经过点
经过点 ,且与直线
,且与直线 垂直,则直线
垂直,则直线 的方程为 .
的方程为 .
“ ”是“不等式
”是“不等式 成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).
成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).
圆心为 ,且经过点
,且经过点 的圆的标准方程为 .
的圆的标准方程为 .
曲线 在点(
在点( )处的切线的斜率为 .
)处的切线的斜率为 .
三棱锥 的侧棱
的侧棱 两两垂直且长度分别为2cm,3cm,1cm,则该三棱锥的体积是 cm3.
两两垂直且长度分别为2cm,3cm,1cm,则该三棱锥的体积是 cm3.
若双曲线 的渐近线方程为
的渐近线方程为 ,则它的离心率为 .
,则它的离心率为 .
已知点P在抛物线 上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
已知圆C经过直线 与坐标轴的两个交点,且经过抛物线
与坐标轴的两个交点,且经过抛物线 的焦点,则圆C的方程为 .
的焦点,则圆C的方程为 .
已知动圆C与圆 及圆
及圆 都内切,则动圆圆心C的轨迹方程为 .
都内切,则动圆圆心C的轨迹方程为 .
已知一个圆锥的母线长为3,则它的体积的最大值为 .
如图,在正方体 中,点
中,点 在面对角线
在面对角线 上运动,给出下列四个命题:
上运动,给出下列四个命题:
① ∥平面
∥平面 ; ②
; ② ;
;
③平面 ⊥平面
⊥平面 ;④三棱锥
;④三棱锥 的体积不变.
的体积不变.
则其中所有正确的命题的序号是 .
若直线 与曲线
与曲线 恰有一个公共点,则实数
恰有一个公共点,则实数 的取值范围为 .
的取值范围为 .
已知椭圆 :
: 的短轴长为2,离心率为
的短轴长为2,离心率为 ,设过右焦点的直线
,设过右焦点的直线 与椭圆
与椭圆 交于不同的两点A,B,过A,B作直线
交于不同的两点A,B,过A,B作直线 的垂线AP,BQ,垂足分别为P,Q.记
的垂线AP,BQ,垂足分别为P,Q.记 , 若直线l的斜率
, 若直线l的斜率 ≥
≥ ,则
,则 的取值范围为 .
的取值范围为 .
已知 为实数,
为实数, :点
:点 在圆
在圆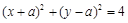 的内部;
的内部; 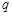 :
: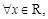 都有
都有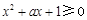 .
.
(1)若 为真命题,求
为真命题,求 的取值范围;
的取值范围;
(2)若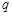 为假命题,求
为假命题,求 的取值范围;
的取值范围;
(3)若“ 且
且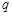 ”为假命题,且“
”为假命题,且“ 或
或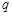 ”为真命题,求
”为真命题,求 的取值范围.
的取值范围.
如图,斜四棱柱 的底面
的底面 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 ,
, 分别为
分别为 的中点.
的中点.
求证:
(1) ;(2)
;(2) ∥平面
∥平面 .
.
已知抛物线 的焦点为双曲线
的焦点为双曲线 的一个焦点,且两条曲线都经过点
的一个焦点,且两条曲线都经过点 .
.
(1)求这两条曲线的标准方程;
(2)已知点 在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点
在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点 的坐标.
的坐标.
已知圆 .
.
(1)若直线 过点
过点 ,且与圆
,且与圆 相切,求直线
相切,求直线 的方程;
的方程;
(2)若圆 的半径为4,圆心
的半径为4,圆心 在直线
在直线 :
: 上,且与圆
上,且与圆 内切,求圆
内切,求圆 的方程.
的方程.
已知函数 ,
, ,
, .
.
(1)若 ,设函数
,设函数 ,求
,求 的极大值;
的极大值;
(2)设函数 ,讨论
,讨论 的单调性.
的单调性.
已知 分别是椭圆
分别是椭圆 的左,右顶点,点
的左,右顶点,点 在椭圆
在椭圆 上,且直线
上,且直线 与直线
与直线 的斜率之积为
的斜率之积为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)点 为椭圆
为椭圆 上除长轴端点外的任一点,直线
上除长轴端点外的任一点,直线 ,
, 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点 ,
, .
.
①在 轴上是否存在一个定点
轴上是否存在一个定点 ,使得
,使得 ?若存在,求点
?若存在,求点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②已知常数 ,求
,求 的取值范围.
的取值范围.