已知全集U={1,2,3,4,5,6,7,8},M ={1,3,5,7},N ={5,6,7},则(CUM)∩ ( CUN)=" " ( )
| A.{5,7} | B.{2,4} | C.{2,4,8} | D.{1,3,5,6,8} |
函数 的定义域是( )
的定义域是( )
A.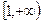 |
B.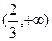 |
C.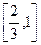 |
D.( ,1) ,1) |
已知点P( )在第三象限,则角
)在第三象限,则角 在 ( )
在 ( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知 与
与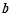 均为单位向量,它们的夹角为60°,那么
均为单位向量,它们的夹角为60°,那么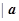 +
+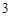
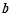 |等于
|等于
A.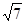 |
B.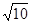 |
C.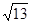 |
D.4 |
.函数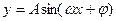 在一个周期内的图象如图所示,此函数的解析式为 ( )
在一个周期内的图象如图所示,此函数的解析式为 ( )
A.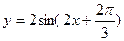 |
B. |
C. |
D. |
幂函数y=x-1及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①、②、③、④、⑤、⑥、⑦、⑧(如右图所示),那么幂函数y=x 的图象经过的“卦限”是
的图象经过的“卦限”是
| A.④⑦ | B.④⑧ | C.③⑧ | D.①⑤ |
将函数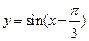 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移
的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移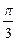 个单位,则所得函数图像对应的解析式为( )
个单位,则所得函数图像对应的解析式为( )
A.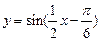 |
B. |
C.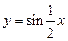 |
D. |
下列各式中,值为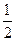 的是( )
的是( )
A. |
B.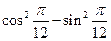 |
C.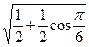 |
D.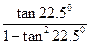 |
已知 为锐角,且cos
为锐角,且cos =
= ,cos
,cos =
=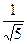 ,则
,则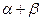 的值是( )
的值是( )
A.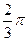 |
B. |
C. |
D.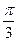 |
函数f(x)= 的零点所在的区间是( )
的零点所在的区间是( ) A
A .(0,
.(0, ) B.(
) B.( ,1) C.(1,
,1) C.(1, ) D.(
) D.( ,2)
,2)
函数 为奇函数,且
为奇函数,且 ,则当
,则当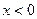 时,
时,
.已知向量 .若向量
.若向量 ,则实数
,则实数 的值是 .
的值是 .
若f(x)= 是(-∞,+∞)上的减函数,则a的取值范围是__
是(-∞,+∞)上的减函数,则a的取值范围是__
.设函数 的图象位于
的图象位于 轴右侧所有的对称中心从左依次为
轴右侧所有的对称中心从左依次为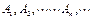 ,则
,则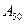 的坐标是 。
的坐标是 。
.下列6个命题中
(1)第一象限角是锐角
(2) 角a终边经过点(a,a)(a¹0)时,sina+cosa=
(3) 若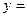
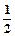
 的最小正周期为
的最小正周期为 ,则
,则
(4)若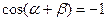 ,则
,则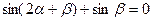
(5) 若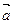 ∥
∥ ,则有且只有一个实数
,则有且只有一个实数 ,使
,使 。
。
(6)若定义在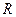 上函数
上函数 满足
满足 ,则
,则 是周期函数请写出正确命题的序号 。
是周期函数请写出正确命题的序号 。
集合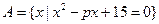 和
和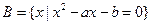 ,若
,若 ,
, ,分别求实数p、a、b的值。
,分别求实数p、a、b的值。
.阅读与理解:
给出公式: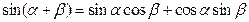 ;
; ;
;
我们可以根据公式将函数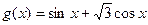 化为:
化为: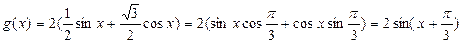
(1)根据你的理解将函数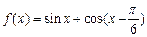 化为
化为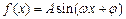 的形式.
的形式.
(2)求出上题函数 的最小正周期、对称中心.
的最小正周期、对称中心.
(3)求函数在区间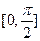 上的最大值、最小值及相应的
上的最大值、最小值及相应的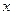 的值。
的值。
设 其中
其中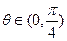 .
.
(1)求 的取值范围;
的取值范围;
(2)若 ,
,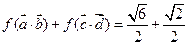 ,求
,求 的值.
的值.
.函数 (
( 为实常数).
为实常数).
(1)若 ,求
,求 的单调区间;
的单调区间;
(2)若 ,设
,设 在区间
在区间 的最小值为
的最小值为 ,求
,求 的表达式
的表达式
.某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/ kg)与上市时间t(单位:天)的数据如下
kg)与上市时间t(单位:天)的数据如下 表:
表:
| 时间t |
50 |
110 |
250 |
| 种植成本Q |
150 |
108 |
150 |
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系,并说明选取该函数的理由。 ,
,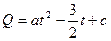 ,
, ,
,
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本。
已知函数
 是奇函数.
是奇函数.
(1)求实数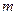 的值;
的值;
(2)判断函数 在
在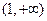 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当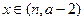 时,函数
时,函数 的值域是
的值域是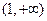 ,求实数
,求实数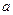 与
与 的值
的值