关于 的方程
的方程 有两个相等的实数根,则
有两个相等的实数根,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知该图案的面积为 ,小正方形的面积为4,若用
,小正方形的面积为4,若用 表示小矩形的两边长,请观察图案,指出以下关系式中不正确的是( )
表示小矩形的两边长,请观察图案,指出以下关系式中不正确的是( )
A. |
B. |
C. |
D. |
若点 是线段
是线段 的黄金分割点,且
的黄金分割点,且 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. |
B. |
C. |
D.以上都不对 |
如图,在△ 中,
中, 为
为 边上一点,∠
边上一点,∠ ∠
∠ ,
, ,
, ,则
,则 的长为( )
的长为( )
| A.1 | B.4 | C.3 | D.2 |
已知等边△ 中,
中, ,
, 与
与 相交于点
相交于点 ,则∠
,则∠ 等于( )
等于( )
| A.75° | B.60° | C.55° | D.45° |
 是关于
是关于 的一元二次方程,则
的一元二次方程,则 的值应为( )
的值应为( )
A. =2 =2 |
B. |
C. |
D.无法确定 |
已知 ,则直线
,则直线 一定经过( )
一定经过( )
| A.第一、二象限 | B.第二、三象限 |
| C.第三、四象限 | D.第一、四象限 |
定义:如果一元二次方程 满足
满足 ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )
A. |
B. |
C. |
D. |
用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中( )
| A.有一个内角大于60° | B.有一个内角小于60° |
| C.每一个内角都大于60° | D.每一个内角都小于60° |
下列命题中是假命题的是( )
A.在△ 中,若 中,若 ,则△ ,则△ 是直角三角形 是直角三角形 |
B.在△ 中,若 中,若 ,则△ ,则△ 是直角三角形 是直角三角形 |
C.在△ 中,若 中,若 ,则△ ,则△ 是直角三角形 是直角三角形 |
D.在△ 中,若 中,若 ,则△ ,则△ 是直角三角形 是直角三角形 |
用反证法证明“ ”时应假设( )
”时应假设( )
A. |
B. |
C. |
D. |
如图,在平行四边形 中,
中, 是
是 的中点,
的中点, 和
和 交于点
交于点 ,设△
,设△ 的面积为
的面积为 ,△
,△ 的面积为
的面积为 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. |
B. |
C. |
D. |
如图,已知 ,若再增加一个条件就能使结论“
,若再增加一个条件就能使结论“ ”成立,则这个条件可以是____________.(只填一个即可)
”成立,则这个条件可以是____________.(只填一个即可)
已知 是方程
是方程 的一个根,则
的一个根,则 的值为______.
的值为______.
如果 ,那么
,那么 的关系是________.
的关系是________.
如果关于 的方程
的方程 没有实数根,则
没有实数根,则 的取值范围为_____________.
的取值范围为_____________.
设 都是正数,且
都是正数,且 ,那么这三个数中至少有一个大于或等于
,那么这三个数中至少有一个大于或等于 .用反证法证明这一结论的第一步是________.
.用反证法证明这一结论的第一步是________.
如图,∠ ∠
∠ ,
, 于
于 ,
, 于
于 ,若
,若 ,
, ,则
,则 ______.
______.
若 (
( 均不为0),则
均不为0),则 的值为 .
的值为 .
在△ABC中, ,
, ,
, ,另一个与它相似的△
,另一个与它相似的△ 的最短边长为45 cm,则△
的最短边长为45 cm,则△ 的周长为________.
的周长为________.
若关于 的一元二次方程
的一元二次方程 的常数项为0,求
的常数项为0,求 的值是多少?
的值是多少?
如果关于 的一元二次方程
的一元二次方程 有实根,求
有实根,求 的取值范围.
的取值范围.
如图,梯形 的中位线
的中位线 与对角线
与对角线 、
、 分别交于
分别交于 ,
, ,
, 求
求 的长.
的长.
如图,点 是正方形
是正方形 内一点,△
内一点,△ 是等边三角形,连接
是等边三角形,连接 ,延长
,延长 交边
交边 于点
于点 .
.
(1)求证:△ ≌△
≌△ ;(2)求∠
;(2)求∠ 的度数.
的度数.
如图,在等腰梯形 中,
中, ∥
∥ ,
, 分别是
分别是 的中点,
的中点, 分别是
分别是 的中点.
的中点.
(1)求证:四边形 是菱形;
是菱形;
(2)若四边形 是正方形,请探索等腰梯形
是正方形,请探索等腰梯形 的高和底边
的高和底边 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
如图,在等腰梯形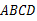 中,
中,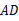 ∥
∥ ,点
,点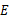 是线段
是线段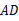 上的一个动点(
上的一个动点(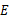 与
与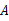 、
、 不重
不重
合),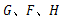 分别是
分别是 的中点.
的中点.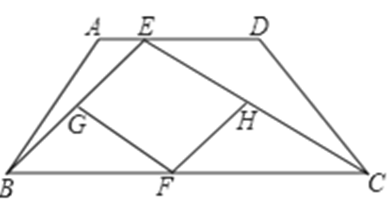
(1)试探索四边形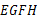 的形状,并说明理由.
的形状,并说明理由.
(2)当点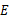 运动到什么位置时,四边形
运动到什么位置时,四边形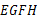 是菱形?并加以证明.
是菱形?并加以证明.
(3)若(2)中的菱形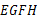 是正方形,请探索线段
是正方形,请探索线段 与线段
与线段 的关系,并证明你的结论.
的关系,并证明你的结论.
已知关于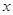 的一元二次方程
的一元二次方程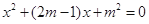 有两个实数根
有两个实数根 和
和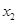 .
.
(1)求实数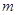 的取值范围;
的取值范围;
(2)当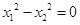 时,求
时,求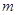 的值.
的值.
如图,点 是菱形
是菱形 的对角线
的对角线 上一点,连接
上一点,连接 并延长,交
并延长,交 于
于 ,交
,交 的延长线于点
的延长线于点 .
.
(1)图中△ 与哪个三角形全等?并说明理由.
与哪个三角形全等?并说明理由.
(2)求证:△ ∽△
∽△ .
.
(3)猜想:线段 ,
, ,
, 之间存在什么关系?并说明理由.
之间存在什么关系?并说明理由.