 ,
, ,则
,则
A. |
B. |
C. |
D. |
 (
( 为虚数单位),则
为虚数单位),则 ( )
( )
A. |
B. |
C. |
D. |
若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. |
B. |
C. |
D. |
根据给出的算法框图,计算 ( )
( )
A. |
B. |
C. |
D. |
某班级统计一次数学测试后的成绩,并制成了如下的频率分布表,根据该表估计该班级的数学测试平均分为( )
| 分组 |
 |
 |
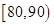 |
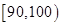 |
| 人数 |
5 |
15 |
20 |
10 |
| 频率 |
0.1 |
0.3 |
0.4 |
0.2 |
(A)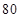 (B)
(B)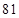 (C)
(C) (D)
(D)
某三棱锥的主视图与俯视图如图所示,则其左视图的面积为
A. |
B. |
C. |
D. |
已知函数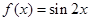 向左平移
向左平移 个单位后,得到函数
个单位后,得到函数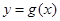 ,下列关于
,下列关于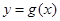 的说法正确的是( )
的说法正确的是( )
A.图象关于点 中心对称 中心对称 |
B.图象关于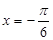 轴对称 轴对称 |
C.在区间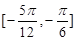 单调递增 单调递增 |
D.在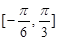 单调递减 单调递减 |
从集合 中随机抽取一个数
中随机抽取一个数 ,从集合
,从集合 中随机抽取一个数
中随机抽取一个数 ,则向量
,则向量 与向量
与向量 垂直的概率为
垂直的概率为
A. |
B. |
C. |
D. |
已知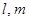 是两条不同的直线,
是两条不同的直线,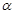 是一个平面,且
是一个平面,且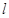 ∥
∥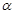 ,则下列命题正确的是( )
,则下列命题正确的是( )
A.若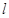 ∥ ∥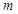 ,则 ,则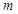 ∥ ∥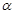 |
B.若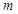 ∥ ∥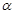 ,则 ,则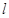 ∥ ∥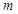 |
C.若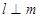 ,则 ,则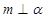 |
D.若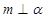 ,则 ,则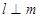 |
双曲线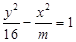 的离心率
的离心率 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
A.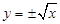 |
B.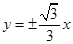 |
C.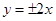 |
D.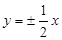 |
函数 为偶函数,且在
为偶函数,且在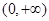 单调递增,则
单调递增,则 的解集为( )
的解集为( )
A. |
B. |
C.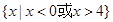 |
D.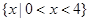 |
已知 ,设函数
,设函数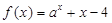 的零点为
的零点为 ,
,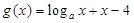 的零点为
的零点为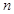 ,则
,则 的最大值为( )
的最大值为( )
A. |
B.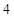 |
C.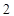 |
D. |
函数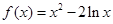 的单调递减区间是____________________.
的单调递减区间是____________________.
已知圆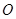 过椭圆
过椭圆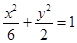 的两焦点且关于直线
的两焦点且关于直线 对称,则圆
对称,则圆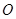 的方程为__________.
的方程为__________.
设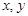 满足约束条件
满足约束条件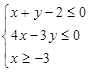 ,则
,则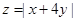 的最大值为_____________.
的最大值为_____________.
函数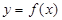 的定义域为
的定义域为 ,其图象上任一点
,其图象上任一点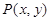 满足
满足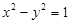 ,则给出以下四个命题:
,则给出以下四个命题:
①函数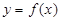 一定是偶函数; ②函数
一定是偶函数; ②函数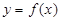 可能是奇函数;
可能是奇函数;
③函数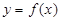 在
在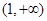 单调递增; ④若
单调递增; ④若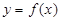 是偶函数,其值域为
是偶函数,其值域为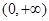
其中正确的序号为_______________.(把所有正确的序号都填上)
已知向量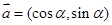 ,
,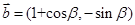 .
.
(1)若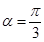 ,
,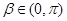 ,且
,且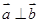 ,求
,求 ;
;
(2)若 ,求
,求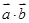 的取值范围.
的取值范围.
某单位招聘职工,经过几轮筛选,一轮从2000名报名者中筛选300名进入二轮笔试,接着按笔试成绩择优取100名进入第三轮面试,最后从面试对象中综合考察聘用50名.
(1)求参加笔试的竞聘者能被聘用的概率;
(2)用分层抽样的方式从最终聘用者中抽取10名进行进行调查问卷,其中有3名女职工,求被聘用的女职工的人数;
(3)单位从聘用的三男和二女中,选派两人参加某项培训,至少选派一名女同志参加的概率是多少?
已知正项数列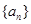 ,其前
,其前 项和
项和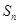 满足
满足 且
且 是
是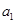 和
和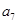 的等比中项..
的等比中项..
(1)求数列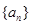 的通项公式;
的通项公式;
(2)设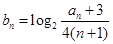 ,求数列
,求数列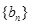 的前99项和.
的前99项和.
如图,矩形 所在的平面和平面
所在的平面和平面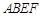 互相垂直,等腰梯形
互相垂直,等腰梯形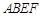 中,
中, ∥
∥ ,
, =2,
=2,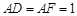 ,
, ,
,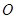 ,
,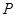 分别为
分别为 ,
,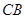 的中点,
的中点,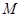 为底面
为底面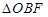 的重心.
的重心.
(1)求证:平面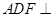 平面
平面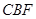 ;
;
(2)求证: 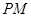 ∥平面
∥平面 ;
;
(3)求多面体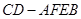 的体积
的体积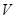 .
.
设函数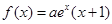 (其中
(其中 ),
), ,已知它们在
,已知它们在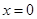 处有相同的切线.
处有相同的切线.
(1)求函数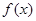 ,
, 的解析式;
的解析式;
(2)求函数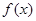 在
在 上的最小值;
上的最小值;
(3)判断函数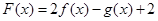 零点个数.
零点个数.
过椭圆 的左顶点
的左顶点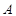 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与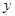 轴的交点为
轴的交点为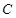 ,已知
,已知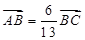 .
.
(1)求椭圆的离心率;
(2)设动直线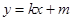 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点 ,且与直线
,且与直线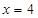 相交于点
相交于点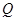 ,若
,若 轴上存在一定点
轴上存在一定点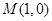 ,使得
,使得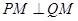 ,求椭圆的方程.
,求椭圆的方程.