已知虚数z满足等式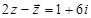 ,则z=
,则z=
若关于x,y的线性方程组的增广矩阵为
 ,该方程组的解为
,该方程组的解为 ,则mn的值等于
,则mn的值等于
直线 的一个法向量可以是
的一个法向量可以是
已知全集 ,则
,则 =
=
某单位有青年职工160人,中年职工人数是老年职工人数的2倍,老、中、青职工共有430人,为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为 .
函数 的反函数是
的反函数是
 中,若
中,若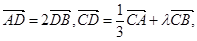 则
则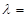
若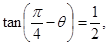 则
则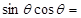
已知函数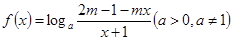 是奇函数,则函数
是奇函数,则函数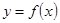 的定义域为
的定义域为
将A、B、C、D四本不同的书分给甲乙丙三个人,每个人至少分到一本书,则不同分法的种数为
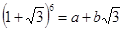 (其中a、b为有理数),则
(其中a、b为有理数),则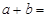
已知双曲线 的左右焦点分别是
的左右焦点分别是 ,设P是双曲线右支上一点,
,设P是双曲线右支上一点, 在
在 上的投影的大小恰好为
上的投影的大小恰好为 ,且它们的夹角为
,且它们的夹角为 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
在实数集R中,我们定义的大小关系“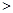 ”为全体实数排了一个序,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“
”为全体实数排了一个序,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“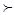 ”,定义如下:对于任意两个复数
”,定义如下:对于任意两个复数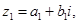

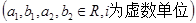 ,
,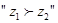 当且仅当
当且仅当 ,下面命题①1
,下面命题①1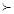 i
i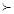 0;②若
0;②若 ,
, ,则
,则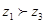 ;③若
;③若 ,则对于任意
,则对于任意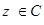 ,
,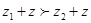 ;④对于复数
;④对于复数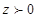 ,则
,则 其中真命题是
其中真命题是
已知 当
当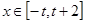 时,函数
时,函数 的最小值为-4,则t的取值范围是
的最小值为-4,则t的取值范围是
设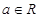 则
则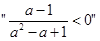 是“
是“ ”成立的 ( )
”成立的 ( )
| A.充分必要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既非充分也非必要条件 |
已知数列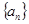 是无穷等比数列,其前n项和是
是无穷等比数列,其前n项和是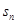 ,若
,若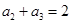 ,
,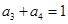 ,则
,则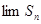 的值为.( )
的值为.( )
A.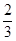 |
B. |
C.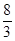 |
D.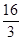 |
对于函数 ,下列选项正确的是 ( )
,下列选项正确的是 ( )
A. 在 在 内是递增的 内是递增的 |
B. 的图像关于原点对称 的图像关于原点对称 |
C. 的最小正周期为2π 的最小正周期为2π |
D. 的最大值为1 的最大值为1 |
已知圆O的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么 的最小值等于.( )
的最小值等于.( )
A. |
B.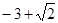 |
C.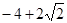 |
D.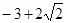 |
(1)解方程: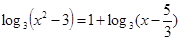
(2)已知命题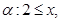 命题
命题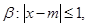 且命题
且命题 是
是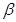 的必要条件,求实数m的取值范围
的必要条件,求实数m的取值范围
在 中,角A、B、C的对边分别为a、b、c,S是该三角形的面积
中,角A、B、C的对边分别为a、b、c,S是该三角形的面积
(1)若 ,
, 求角B的度数
求角B的度数
(2)若a=8,B= ,S=
,S= ,求b的值
,求b的值
已知圆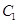 的圆心在坐标原点O,且恰好与直线
的圆心在坐标原点O,且恰好与直线 相切.
相切.
(1)求圆的标准方程;
(2)设点A为圆上一动点,AN
 轴于N,若动点Q满足
轴于N,若动点Q满足 (其中m为非零常数),试求动点
(其中m为非零常数),试求动点 的轨迹方程
的轨迹方程 .
.
(3)在(2)的结论下,当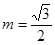 时,得到动点Q的轨迹曲线C,与
时,得到动点Q的轨迹曲线C,与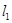 垂直的直线
垂直的直线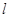 与曲线C交于 B、D两点,求
与曲线C交于 B、D两点,求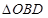 面积的最大值.
面积的最大值.
已知数列 的前n项的和为
的前n项的和为 ,且
,且 ,
,
(1)证明数列 是等比数列
是等比数列
(2)求通项 与前n项的和
与前n项的和 ;
;
(3)设 若集合M=
若集合M= 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围.
已知函数 对任意的
对任意的 恒有
恒有 成立.
成立.
(1)当b=0时,记 若
若 在
在 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;
(2)证明:当 时,
时, 成立;
成立;
(3)若对满足条件的任意实数b,c,不等式 恒成立,求M的最小值.
恒成立,求M的最小值.