已知数列{ }的通项公式是
}的通项公式是 =
= (
( ),则数列的第5项为( )
),则数列的第5项为( )
A. |
B. |
C. |
D. |
在 中,
中, ,则A等于( )
,则A等于( )
A
不等式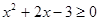 的解集为( )
的解集为( )
A.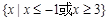 |
B.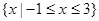 |
C. |
D.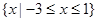 |
在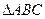 中,
中,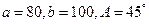 ,则此三角形解的情况是( )
,则此三角形解的情况是( )
| A.一解 | B.两解 | C.一解或两解 | D.无解 |
某种细菌在培养过程中,每20分钟分裂一次(一个分裂二个)经过3小时,这种细菌由1个可以繁殖成( )
| A.511个 | B.512个 | C.1023个 | D.1024个 |
数列{ }的通项公式是
}的通项公式是 =
= (
( ),那么
),那么 与
与 的大小关系是( )
的大小关系是( )
A. > > |
B. < < |
C. = = |
D.不能确定 |
关于x的不等式 ,则关于x的不等式
,则关于x的不等式 的解集为( )
的解集为( )
| A.(-2,1) | B. |
| C.(-2,-1) | D. |
两个等差数列 和
和 ,其前
,其前 项和分别为
项和分别为 ,且
,且 则
则 等于
等于
A. |
B. |
C. |
D. |
已知点P(x,y)在不等式组 表示的平面区域上运动,则z=x-y的取值范围是( )
表示的平面区域上运动,则z=x-y的取值范围是( )
| A.[-2,-1] | B.[-2,1] | C.[-1,2] | D.[1,2] |
等差数列 中,
中, 则使前
则使前 项和
项和 成立的最大自然数
成立的最大自然数 为
为
| A.4005 | B.4006 | C.4007 | D.4008 |
数列 1 , 2
, 2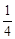 , 3
, 3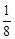 , 4
, 4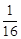 , 5
, 5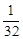 , …, 的前n项之和等于 .
, …, 的前n项之和等于 .
已知数列 的前n项和
的前n项和 ,那么它的通项公式为
,那么它的通项公式为 ________
________
在△ABC中,B=135°,C=15°,a=5,则此三角形的最大边长为 .
已知 ,则
,则 的最小值是 .
的最小值是 .
某人向银行贷款A万元用于购房。已知年利率为r,利息要按复利计算(即本年的利息计入次年的本金生息)。如果贷款在今年11月7日完成,则从明年开始,每年的11月6日向银行等额还款a万元,n年还清贷款(及利息)。则a= (用A、r和n表示)。
把正整数按上小下大、左小右大的原则排成如图三角形数
表(每行比上一行多一个数):设 (i、j∈N*)是位于
(i、j∈N*)是位于
这个三角形数表中从上往下数第i行、从左往右数第j个数,
如 =8.若
=8.若 =2006,则i、j的值分别为________ ,__________
=2006,则i、j的值分别为________ ,__________
已知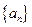 是等差数列,其中
是等差数列,其中
(1)求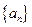 的通项公式
的通项公式
(2)数列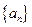 从哪一项开始小于0;
从哪一项开始小于0;
(3)求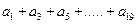 值。
值。
在△ABC中,BC=a,AC=b,a,b是方程 的两个根,且
的两个根,且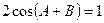 。
。
求:(1)角C的度数; (2)AB的长度。
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n N+,都有
N+,都有 。
。
(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设 ,
, 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得 对所有n
对所有n N+都成立的最小正整数
N+都成立的最小正整数 的值。
的值。