函数
的零点是（ ）
A． |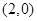
B． |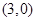
C． |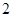
D． |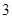
已知直线
的方程为
，则直线的倾斜角为（ ）
A． |
B． |
C． |
D．与 有关 |
空间四点最多可确定平面的个数是（ ）
A． |
B． |
C． |
D． |
函数
的定义域是（ ）
A． |
B． |
C． |
D． |
若直线
与直线
平行，则
的值为（ ）
A． |
B． |
C． |
D． |
右图中的三个直角三角形是一个体积为
的几何体的三视图，则
（ ）
A． |
B． |
C． |
D． |
已知点
在直线
上，则
的最小值为（ ）
A． |
B． |
C． |
D． |
设
是两条不同的直线，
是三个不同的平面，则下列命题正确的是（ ）
A．若 ， ，则 |
B．若与 所成的角相等，则 |
C．若 ， ，则 |
D．若， ，则 |
设
，则
，
，
的大小关系是（ ）
A． |
B． |
C． |
D． |
在
中，
，
，
，若把绕直线
旋转一周，则所形成的几何体的体积是（ ）
A． |
B． |
C． |
D． |
如图，有一块等腰直角三角形
的空地，要在这块空地上开辟一个内接矩形
的绿地，已知
,
，绿地面积最大值为（ ）
A． |
B． |
C． |
D． |
已知函数
对于满足
的任意
，
，给出下列结论：
①
②
③
④
其中正确的是（ ）
| A．①③ | B．①④ | C．②③ | D．②④ |
已知正方体外接球表面积是
，则此正方体边长为
已知集合
，集合
，若
是单元素集，则
=
设
是奇函数，且在
内是减函数，又
，则
的解集是
如图是从上下底面处在水平状态下的棱长为
的正方体
中分离出来的.
有如下结论：
①
在图中的度数和它表示的角的真实度数都是
；
②
；
③
与
所成的角是
；
④若
，则用图示中这样一个装置盛水，最多能盛
的水.
其中正确的结论是 （请填上你所有认为正确结论的序号）.
已知
，
.
（1）求
和
；
（2）定义
且
，求
和
.
已知圆
：
内有一点
，过点
作直线
交圆于
，
两点.
（1）当经过圆心时，求直线的方程；
（2）当弦
被点平分时，写出直线的方程.[
已知一个几何体的三视图如图所示.
（1）求此几何体的表面积；
（2）在如图的正视图中，如果点
为所在线段中点，点
为顶点，求在几何体侧面上从点到点的最短路径的长.
已知以点
为圆心的圆经过点
和
，且圆心在直线
上.
（1）求圆的方程；
（2）设点
在圆上，求
的面积的最大值.
如图，四棱锥
，底面
是矩形，平面
底面，
，
平面
，且点
在
上.
（1）求证：
；
（2）求三棱锥
的体积；
（3）设点
在线段
上，且满足
，试在线段上确定一点
，使得
平面
.
已知二次函数
在区间 
上有最大值
，最小值
.
（1）求函数
的解析式；
（2）设
.若
在
时恒成立，求
的取值范围.