命题“存在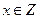 ,使
,使 ”的否定是( ).
”的否定是( ).
A.存在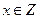 ,使 ,使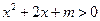 |
B.不存在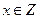 ,使 ,使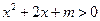 |
C.对于任意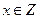 ,都有 ,都有 |
D.对于任意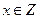 ,都有 ,都有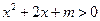 |
在ΔABC 中,若 sinA >sinB,则( ).
A. > > |
B. < < |
C.   |
D.   |
等差数列{an}中,已知前15项的和 ,则
,则 等于( ).
等于( ).
A. |
B.12 | C. |
D.6 |
已知 ,则
,则 ( ).
( ).
A. B.
B. C.
C. D.
D.
A. B.
B. C.
C. D.
D. 
设定点 与抛物线
与抛物线 上的点
上的点 的距离为
的距离为 ,
, 到抛物线焦点F的距离为
到抛物线焦点F的距离为 ,则
,则 取最小值时,
取最小值时, 点的坐标为( ).
点的坐标为( ).
A. |
B. |
C. |
D. |
若“ ”和“
”和“ ”都是假命题,其逆命题都是真命题,则“
”都是假命题,其逆命题都是真命题,则“ ”是“
”是“ ”的( ).
”的( ).
| A.必要非充分条件 | B.充分非必要条件 |
| C.充分必要条件 | D.既非充分也非必要条件 |
二次函数 则实数a的取值( ).
则实数a的取值( ).
| A.-2<a<1 | B.-1<a< 1 |
| C.0<a<1 | D.0<a<2 |
若 ,则下列不等式①
,则下列不等式① ;②
;② ③
③ ;④
;④ 中,正确的不等式有( ).
中,正确的不等式有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
要得到函数 的图像,只需要将函数
的图像,只需要将函数 的图像 ( ).
的图像 ( ).
A.向右平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向左平移 个单位 个单位 |
已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的公比和项数分别为( )
| A.8,2 | B.2,4 | C.4,10 | D.2,8 |
在ΔABC中,cos =
= ,则ΔABC的形状为( ).
,则ΔABC的形状为( ).
| A.正三角形 | B.直角三角形 |
| C.等腰三角形或直角三角形 | D.等腰直角三角形 |
若椭圆 和双曲线
和双曲线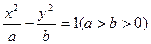 有相同的左、右焦点
有相同的左、右焦点 ,P是两条曲线的一个交点,则
,P是两条曲线的一个交点,则 的值是( ).
的值是( ).
A. |
B. |
C.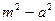 |
D.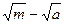 |
 .
.
“有个实数 是方程
是方程 的根”此命题的否定是:
的根”此命题的否定是:
(用符号“ ”与“
”与“ ”表示)
”表示)
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a1等于 .
与双曲线 有共同渐近线且焦距为12的双曲线的标准方程为
有共同渐近线且焦距为12的双曲线的标准方程为
_______________________.
已知等比数列 前
前 项之和为
项之和为 ,
,  ,
, ,求
,求 和
和
在 中,
中, 所对的边长分别为
所对的边长分别为 ,设
,设 满足条件
满足条件 和
和 ,
,
(1)求角A的大小;
(2)求 的值.
的值.
已知函数f(t)=
(1)求f(t)的值域G;
(2)若对于G内的所有实数x,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
已知 ,
, .
.
(1)若 ,求
,求 的值.
的值.
(2)若 ,求
,求 的单调的递减区间;
的单调的递减区间;
已知椭圆 过点
过点 离心率
离心率 ,
,
(1)求椭圆方程;
(2)若过点 的直线
的直线 与椭圆C交于A、B两点,且以AB为直径的圆过原点,试求直线
与椭圆C交于A、B两点,且以AB为直径的圆过原点,试求直线 的方程。
的方程。
设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的格点(格点即横坐标和纵坐标均为整数的点)的个数为
内的格点(格点即横坐标和纵坐标均为整数的点)的个数为 .
.
(1)写出 、
、 、
、 的值及
的值及 的表达式;
的表达式;
(2)设 ,
, 为
为 的前
的前 项和,求
项和,求 ..
..