设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ=______
已知 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
在△ABC中,  则
则 = ( )
= ( )
A. |
B. |
C. |
D. |
若 ,则
,则
已知△ABC的内角A、B、C所对应边分别为a、b、c,若 ,则角C的大小是_______________(结果用反三角函数值表示)
,则角C的大小是_______________(结果用反三角函数值表示)
设△ABC的内角A, B, C所对的边分别为a, b, c, 若 , 则△ABC的形状为 ( )
, 则△ABC的形状为 ( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不确定 |
将函数 的图象沿轴向左平移
的图象沿轴向左平移 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则 的一个可能取值为
的一个可能取值为
A. |
B. |
C. |
D. |
已知点
A. |
B. |
C. |
D. |
在 ,内角
,内角 所对的边长分别为
所对的边长分别为


A. |
B. |
C. |
D. |
函数y=sin2x+2 sin2x的最小正周期T为_______.
sin2x的最小正周期T为_______.
设θ为第二象限角,若tan(θ+ )=
)= ,则sinθ+cosθ=_________.
,则sinθ+cosθ=_________.
如图,半径为1的半圆O与等边三角形ABC夹在两平行线ι1,ι2之间,ι//ι1,ι与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点。
设弧FG的长为x(0<x<π),y=EB+BC+CD,若ι从ι1平行移动到ι2,则函数y=f(x)的图像大致是

在等腰三角形 中,
中, 点
点 是边
是边 上异于
上异于 的一点,光线从点
的一点,光线从点 出发,经
出发,经 发射后又回到原点
发射后又回到原点 (如图).若光线
(如图).若光线 经过
经过 的中心,则
的中心,则 等于( )
等于( )

A. |
B. |
C. |
D. |
在锐角中 ,角
,角 所对的边长分别为
所对的边长分别为 .若
.若 ( )
( )
A. |
B. |
C. |
D. |
已知 是第三象限角,
是第三象限角, ,则
,则
已知函数 ,下列结论中错误的是( )
,下列结论中错误的是( )
A. 的图像关于点 的图像关于点 中心对称 中心对称 |
B. 的图像关于直线 的图像关于直线 对称 对称 |
C. 的最大值为 的最大值为 |
D. 既是奇函数,又是周期函数 既是奇函数,又是周期函数 |
在△ABC中,a=3,b=2 ,∠B=2∠A.
,∠B=2∠A.
(1)求cosA的值,
(2)求c的值
 中,
中, ,
, 是
是 的中点,若
的中点,若 ,则
,则 ________。
________。
设 的内角
的内角 所对边的长分别为
所对边的长分别为 。若
。若 ,则
,则 则角
则角 _________.
_________.
已知函数
 的最小正周期为
的最小正周期为 。
。
(1)求 的值;
的值;
(2)讨论 在区间
在区间 上的单调性。
上的单调性。
△ABC在内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB。
(1)求B;
(2)若b=2,求△ABC面积的最大值。
设 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c, .
.
(1)求B;
(2)若 ,求C.
,求C.
已知函数 的周期为
的周期为 ,图象的一个对称中心为
,图象的一个对称中心为 ,将函数
,将函数 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个 单位长度后得到函数
单位长度后得到函数 的图象。
的图象。
(1)求函数 与
与 的解析式
的解析式
(2)是否存在 ,使得
,使得 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;
(3)求实数 与正整数
与正整数 ,使得
,使得 在
在 内恰有2013个零点
内恰有2013个零点
已知函数 ,
, .
.
(1) 求 的值;
的值;
(2) 若 ,
, ,求
,求 .
.
已知函数 。
。
(1)若 是第一象限角,且
是第一象限角,且 。求
。求 的值;
的值;
(2)求使 成立的x的取值集合。
成立的x的取值集合。
在△ABC中,角A,B,C所对的边分别为a,b,c,已知
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
已知函数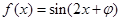 ,其中
,其中 为实数,若
为实数,若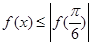 对
对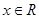 恒成立,且
恒成立,且 ,则
,则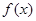 的单调递增区间是
的单调递增区间是
A.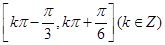 |
B.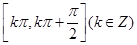 |
C.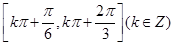 |
D. |
△ABC的三个内角A、B、C所对的边分别为a,b,c,asin AsinB+bcos2A= 则
则 ( )
( )
(A)  (B)
(B)  (C)
(C)  (D)
(D)
设sin ,则
,则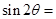 ( )
( )
A. |
B. |
C.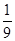 |
D.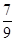 |
若 ,
, ,
, ,
, ,则
,则
A. |
B. |
C. |
D. |
函数 在
在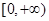 内
内
| A.没有零点 | B.有且仅有一个零点 |
| C.有且仅有两一个零点 | D.有无穷个零点 |
若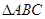 的内角
的内角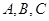 所对的边
所对的边 满足
满足 ,且
,且 ,则
,则 的值为
的值为
A. |
B.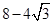 |
| C.1 | D.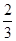 |
将函数 的图象向右平移
的图象向右平移 个单位,再向上平移1个单位,所得函数图象对应的解析式为 ( )
个单位,再向上平移1个单位,所得函数图象对应的解析式为 ( )
A. |
B. |
C. |
D. |
在 中,若
中,若 ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
在锐角 中,AB=3,AC=4,其面积
中,AB=3,AC=4,其面积 ,则BC=( )
,则BC=( )
A. |
B. 或 或 |
C. |
D. |
在 ,则
,则 的值是( )
的值是( )
A. |
B.1 | C. |
D.2 |
在 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 ,且
,且 ,则
,则 的值为( )
的值为( )
| A.5 | B.6 | C. |
D. |
函数 (其中A>0,
(其中A>0, )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将g(x)=sin2x的图象( )
的图象,则只需将g(x)=sin2x的图象( )

A.向右平移 个长度单位 个长度单位 |
B.向左平移 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 |
D.向左平移 个长度单位 个长度单位 |
将函数f(x)= 的图象向左平移m个单位(m>0),若所得的图象关于直线x=
的图象向左平移m个单位(m>0),若所得的图象关于直线x= 对称,则m的最小值为( )
对称,则m的最小值为( )
A. |
B. |
C. |
D. |
若关于 的方程
的方程 在区间
在区间 上有两个不同的实数解,则
上有两个不同的实数解,则 的取值范围为
的取值范围为
在△ABC中,内角A、B、C的对边长分别为a、b、c,已知 ,且
,且 ,
,
则b= .
已知 ,则
,则 = .
= .
在 中,
中, 分别为角
分别为角 的对边,若
的对边,若 ,且
,且 ,则边
,则边 等于 .
等于 .
如图,函数 (其中
(其中 ,
, ,
, )与坐标轴的三个交点
)与坐标轴的三个交点 、
、 、
、 满足
满足 ,
, ,
, 为
为 的中点,
的中点, , 则
, 则 的值为____________
的值为____________
已知 为钝角,
为钝角, 则
则 _________.
_________.
在DABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5, .
.
(1) 求 和
和 的值;
的值;
(2) 设函数 ,求
,求 的值.
的值.
在 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,求
,求 的面积.
的面积.
在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 的面积.
的面积.
已知在△ABC中,角A,B,C的对边分别是a,b,c,满足 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
(1)求角A的值;
(2)求f(C)=2sinC·cosB的值域.
已知函数 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
.
(1)求 的值;
的值;
(2)在 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,求
,求 的取值范围.
的取值范围.
已知△ABC中的内角A,B,C对边分别为a,b,c, sin2C+2cos2C+1=3,c=
sin2C+2cos2C+1=3,c= .
.
(1)若cosA= ,求a;
,求a;
(2)若2sinA=sinB,求△ABC的面积.
在 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求 的值;
的值;
(2)若 成等差数列,且公差大于0,求
成等差数列,且公差大于0,求 的值.
的值.
已知向量 ,
, ,且
,且 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调递增区间;
的单调递增区间;
(2)已知 分别为
分别为 的三个内角
的三个内角 对应的边长,若
对应的边长,若 ,且
,且 ,
, ,求
,求 的面积.
的面积.