设a,b,m都是正数,且a<b,则下列不等式中恒成立的是 ( )
A． < <1 |
B．≥ |
| C．≤≤1 |
D．1<< |
“a>1”是“
<1”的 ( )
| A．充分但不必要条件 | B．必要但不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
设a,b∈R+,A=
+
,B=
,则A,B的大小关系是 ( )
| A．A≥B | B．A≤B |
| C．A>B | D．A<B |
已知a>b>0,c>d>0,m=
-
,n=
,则m与n的大小关系是( )
| A．m<n | B．m>n | C．m≥n | D．m≤n |
已知下列不等式:①x2+3>2x;②a5+b5>a3b2+a2b3;③a2+b2≥2(a-b-1).
其中正确的个数为 ( )
| A．0 | B．1 | C．2 | D．3 |
设a>0,b>0,下列不等式中不正确的是 ( )
| A．a2+b2≥2ab | B． + ≥2 |
C． + ≥a+b |
D． + ≤ |
在等比数列{an}和等差数列{bn}中,a1=b1>0,a3=b3>0,a1≠a3,则a5与b5的大小关系为 ( )
| A．a5>b5 | B．a5<b5 |
| C．a5=b5 | D．不确定 |
已知0<x<1,a=2
,b=1+x,c=
,则其中最大的是 .
若x是正数,且x3-x=2,则x与
的大小关系为 .
设A=
+
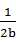,B=
(a>0,b>0),则A,B的大小关系为 .
已知a>0,b>0,求证:
+
≥
+
.
若a,b,m,n都为正实数,且m+n=1.
求证:
≥m
+n
.
已知函数f(x)=x2+ax+b,当p,q满足p+q=1时,证明:pf(x)+qf(y)≥f(px+qy)对于任意实数x,y都成立的充要条件是0≤p≤1.
设a>0,b>0且ab-(a+b)≥1,则 ( )
A．a+b≥2( +1) |
B．a+b≤+1 |
| C．a+b≤(+1)2 |
D．a+b>2(+1) |
若1<x<10,下面不等式中正确的是 ( )
| A．(lgx)2<lgx2<lg(lgx) |
| B．lgx2<(lgx)2<lg(lgx) |
| C．(lgx)2<lg(lgx)<lgx2 |
| D．lg(lgx)<(lgx)2<lgx2 |
下列三个不等式中:①a<0<b;②b<a<0;③b<0<a,其中能使
<
成立的充分条件有 ( )
| A．①② | B．①③ | C．②③ | D．①②③ |
要证a2+b2-1-a2b2≤0,只要证 ( )
| A．2ab-1-a2b2≤0 |
B．a2+b2-1- ≤0 |
C． -1-a2b2≤0 |
| D．(a2-1) (b2-1)≥0 |
已知a,b,c为三角形的三边且S=a2+b2+c2,P=ab+bc+ca,则 ( )
| A．S≥2P | B．P<S<2P |
| C．S>P | D．P≤S<2P |
设x1和x2是方程x2+px+4=0的两个不相等的实数根,则 ( )
| A．|x1|>2且|x2|>2 | B．|x1+x2|<4 |
| C．|x1+x2|>4 | D．|x1|=4且|x2|=1 |
等式“
=
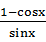”的证明过程:“等式两边同时乘以
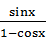得,左边=·=
=
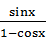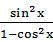=1,右边=1,左边=右边,故原不等式成立”,应用了
的证明方法.(填“综合法”或“分析法”)
设x,y,z为正实数,满足x-2y+3z=0,则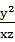
的最小值是 .
设a,b,c都是正实数,a+b+c=1,则
+
+
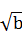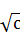的最大值为 .
用分析法证明:当x>0时,sinx<x.
用分析法证明:当x>1时,x>ln(1+x).
已知x,y,z均为正数,求证:
+
+
≥
+
+
.
在某两个正数x,y之间,若插入一个数a,使x,a,y成等差数列,若插入两个数b,c,使x,b,c,y成等比数列,求证:(a+1)2≥(b+1)(c+1).